Perrin's Sequence

Define the sequence of integers by the linear recurrence formula

               s[n] = s[n-2] + s[n-3]

with the initial values  s[0] = 3, s[1] = 0 , s[2] = 2.  This 
sequence was discussed by Edouard Lucas in 1878 (American Journal 
of Mathematics, vol 1, page 230ff), who noted that if p is a prime 
then p divides s[p].  This is an immediate consequence of Fermat's 
Little Theorem, and as such is a necessary but not sufficient 
condition for primality (see proof).  Subsequently (1899) the 
same sequence was mentioned by R. Perrin (L'Intermediaire Des 
Mathematiciens).  The most extensive (published) treatment of this 
sequence was given in an excellent paper by Dan Shanks and Bill 
Adams in 1982 (Mathematics of Computation, vol 39, n. 159).  
[Sadly, Dan Shanks passed away just recently at the age of 80.]
Shanks and Adams referred to this as Perrin's sequence.

This sequence has many interesting properties, making it, in some
ways, more remarkable than the Fibonacci sequence.  For example,
most people are familiar with the spiral of equilateral squares 
whose edge lengths correspond to the Fibonacci numbers, but less
well-known is the spiral of equilateral triangles shown below
described in The Golden Pentagon.

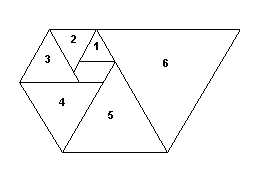The edge lengths of successive triangles in this spiral satisfy the 
Perrin recurrence s[n]=s[n-2]+s[n-3] as well as the recurrence 
s[n]=s[n-1]+s[n-5], as is apparent from the above figure.  This can 
be seen as a consequence of the fact that the characteristic polynomial 
of Perrin's sequence, x^3 - x - 1, is a divisor of the characteristic 
polynomial of the 5th order sequence, i.e.,

            x^5 - x^4 - 1  =  (x^3 - x - 1)(x^2 - x - 1)

Interestingly, the real root r of x^3 - x - 1 has the nice expression
as a sequence of nested cube roots:
             ___________________________
           3/         ____________________
   r  =    /        3/        _________________
         \/   1 +   /       3/        _______________
                  \/  1 +   /       3/
                          \/  1 +   /
                                  \/  1 + ...

       =  1.324717957244746...

If we define the angle q in terms of this root r as
      
                       / -1   3/2 \
          q  =  invcos(  --- r     )  =  2.437734932...
                       \  2       /

then the terms of the Perrin sequence can be expressed in closed 
form as
                      n         cos(nq)
            s[n]  =  r   +   2 ---------
                                r^(n/2)

In fact, with the appropriate provisos, we can replace n with any
complex argument z to define Perrin's function on the complex plane,
as shown in the figure below for real components from -5 to 15 and
imaginary components from -5 to +5.



White indicates regions where both the real and imaginary components 
are positive, black where both are negative, and the two shades of 
gray where one is positive and the other negative.  The zeros of this 
function are all on the real axis in the left half-plane, whereas 
there are two sets of complex conjugate zeros on the right half-plane 
(at points where all four shades meet).

Obviously, for any positive prime p and any integer n we have

               s[pn] = s[n]   (mod p)

so in particular we have

                 s[p] = 0   
                                (mod p)
                s[-p] = -1

In addition, for any integers m,n,k we have the relation

    s[mn+k] = s[m]s[m(n-1)+k] - s[-m]s[m(n-2)+k] + s[m(n-3)+k]

Which is really just a special case of a much more general class of
relations satisfied by any linear recurring sequence.  (See the note
Identities for Linear Recurring Sequences.)  In this particular 
case we have relations like

             s[2n] = s[n]^2 - 2s[-n]

            s[3n] = s[n]^3 - 3s[n]s[-n] + 3

and so on, as well as

           s[2n+1] = s[n]s[n+1] + s[1-n]

Using these relations for s[2n] and s[2n+1] gives an efficient means
of computing s[k] via the usual binary pattern algorithm on the plus
and minus sides of the sequence.  This same two-sided approach can
be extended to higher order recurrences, but it quickly becomes more
practical to use the more general one-sided relations (described in 
the note mentioned above).

Perrin's sequence also has the interesting property that its terms
are cumulative sums of the sequence itself, i.e., we have s[1]=0 and

                          n-5
                  s[n] = SUM   s[k]          for n > 1
                          k=-3


                          4-n
                  s[n] = SUM   s[-k]         for n < 1
                          k=4


The terms of Perrin's sequence can also be expressed as a function
of binomial coefficients, leading to many interesting results.  For
example, it's possible to deduce that the summation

                    N        (2N+k)!
                 SUM     ----------------
                   k=0   (2N-2k)! (1+3k)!

is an integer for N=2755452, and for no smaller N.  (See the note
Summations and Recurrences.)

As a compositeness test, Perrin's sequence is much stronger than the
typical 2nd order Lucas sequence.  For example, the smallest symmetric
pseudoprime relative to the Fibonacci quadratic x^2 - x- 1 is 705, 
whereas the smallest realtive to Perrin's cubic x^3 - x - 1 is

                     27664033 = (3037)(9109)

as found by Shanks and Adams (using an HP-41C calculator!).  
Subsequently Shanks, G. Kurtz, and H. Williams tabulated all the
symmetric pseudoprimes relative to Perrin's sequence less than
50(10)^9.  They noted that none of these pseudoprimes had the 
signature of a prime p such that Perrin's polynomial is irreducible 
(mod p).  As far as I know the question of whether such a pseudoprime 
exists is still open.

Further discussion of pseudoprimes relative to various polynomials
can be found in the notes

   Pseudoprimes for x^2 - 4x - 9
   Lucas and Perrin Pseudoprimes
   Symmetric Pseudoprimes