The Golden Pentagon

The plane can be tiled by a geometric progression of equilateral 
triangles with the characteristic equation x^3 - x - 1 as shown 
below


In view of the popularity of the "golden rectangle" based on 
the geometric spiral of squares, it's surprising the analagous 
construction for equilateral triangles is rarely mentioned.  
Another picture, this one with the triangles numbered in
sequence, is shown below.

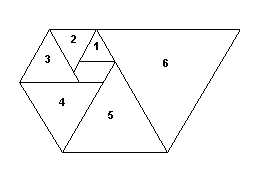Notice that if h(k) denotes the height of the kth triangle
in the spiral, then each of the following recurrences is
satisfied
             h(k)  =  h(k-1) + h(k-5)

             h(k)  =  h(k-2) + h(k-3)

This corresponds to the fact that the sequence has two possible
characteristic equations

                 x^5 - x^4 - 1  =  0

                  x^3 - x - 1  =  0

This isn't surprising, because the second polynomial is a
divisor of the first, i.e.,

       (x^5 - x^4 - 1)  =  (x^3 - x - 1)(x^2 - x + 1)

Each triangle in the sequence is larger than the preceeding
triangle by a factor w, defined as the real root of the
cubic factor x^3 - x - 1.  This value can be expressed as

          / 1    /  1       1  \1/2 \1/3
   w  =  (  - + (  ---  -  ---  )    )
          \ 2    \ 2^2     3^3 /    /

                        / 1    /  1       1  \1/2 \1/3
                    +  (  - - (  ---  -  ---  )    )
                        \ 2    \ 2^2     3^3 /    /

The numerical value of this "other golden proportion" is

                  w = 1.324717957244746...

For more on this ratio and related numerical sequences, see the
note on Perrin's Sequence.