On the Cumulative Results of Quantum Measurements

Suppose a spin-zero particle decays into two spin-1/2 particles.
Conservation of angular momentum evidently requires that the "spin
vectors" of the two particles sum to zero.  More precisely, if the
spins of these two particles are measured with respect to any given
angle, the particles will necessarily exhibit opposite spins.  Thus,
the "exhibited spin vectors" point in opposite directions parallel
to the measurement angle, and their vector sum is zero.

However, suppose we measure the spins of these two particles with
respect to different angles.  We know that if a particle's spin is
"measured" along a certain axis, it will necessarily "exhibit" spin
that corresponds to a vector parallel to the axis of measurement, in
either the positive or negative sense.  Thus, by measuring the spins
of the two particles along different axes we can ensure that their
exhibited spins are not parallel, so they cannot sum to zero.

In this way we can begin with a spin-zero particle and end up with
two particles that interact with the surroundings by exhibiting 
spins whose vector sum is NON-zero.  It might be thought that this 
presents a problem for the conservation of angular momentum, but of 
course the two particles continue to possess spin following their 
interactions with the measuring devices, so the "total spin" imparted 
to the surroundings is not just the vector sum of the spins exhibited 
by the two initial measurements.  One could also point out that a
quantum spin "exibition" doesn't actually impart quantum spin to
the surroundings, so the conservation at issue is more subtle.

However, if we take the attitude that "spin is as spin does", 
we could perhaps argue that the vector sum of ALL future "spin 
exhibitions" by those two particles must be zero.  Admittedly, the 
empirical content of this assertion is questionable, because we 
can never actually evaluate the sum, at least not prior to the 
"completion" of the universe (by which time we probably won't 
care). Nevertheless, it's interesting to note that in order for 
the universe to actually impose such a condition it would need 
to place constraints not only on the behavior of the particles 
themselves but also on the *circumstances* they encounter.

For example, if one of the particles is measured once along a
direction x, it would not be acceptable for all other exhibitions
of spin of the two particles to be along an axis perpindicular to
x, because then the results could never sum to zero.  Thus a
principle of conservation of "exhibited spin vectors" would imply
eventual restrictions on our "choice" of measurement angles as
well as on the particles' responses to those angles.

It might be argued that we could accept violations of this 
postulated conservation law as long as they were within the 
original quantum uncertainty limits, and that this tolerance 
might be adequate to eliminate any effective requirements on 
the "environment".  However, it appears that if we simply monitor 
the exhibited spins of the two particles for a period of time, the 
net vector sum would essentially be a random walk, which can reach 
positions arbitrarily far from "zero" in any particular direction.  
This would then require the environment to give those particles a 
sufficient number of opportunities to exhibit spin along that 
direction, so that it can ultimately get back to (or even close 
to) zero.

In any case, it's interesting that the "net spin vector" resulting
from (the initial) measurements of the two spin-1/2 particles 
discussed above is different depending on whether you assume the 
pair correlations predicted by QM or those predicted by a typical 
"realistic" model.  If we represent the individual exhibited spin 
vectors by unit complex numbers and assign one of the measurement 
directions to the number 1, we can express the "net spin vector" 
for a given difference q between the two measurement axes as

  S(q) = (1 + exp(iq)) C(q) + (1 + exp(i(q+pi))) (1 - C(q))

where C(q) is the correlation between the two measurements with a 
difference angle of q.  This is just the weighted average of the 
two possible outcomes for this value of q.  This reduces to

                S(q) = 1 + (2C(q) - 1) exp(iq)

Our two candidates for the correlation function C(q) are

                /  (1 - cos(q))/2           Quantum Mechanics
        C(q) = (
                \   1 - |(q-pi)/pi)|        Simple Realistic

Substituting these into the preceeding equation for S(q) gives the
expressions for the net spin vector resulting from combined spin 
measurements on two coupled particles

           /  1  -  cos(q) exp(iq)               Quantum Mechanics
   S(q) = (
           \  1 - (1 - 2|(q-pi)/pi|) exp(iq)    Simple Realistic

Splitting up these expressions into their real and imaginary parts 
we have

         /             [sin(q)^2] - i [sin(q)cos(q)]
 S(q) = (
         \[1+(1-2|(q-pi)/pi|)cos(q)] + i [(1-2|(q-pi)/pi|)sin(q)]

We could then multiply each of these by exp(iw) where w is the angle
of our first measurement (which we arbitrarily assigned to the number 
1), but this just shows that there is circular symmetry of the overall 
outcome, so we'll focus on just the relative distribution of net spin 
vectors.  The results are illustrated below.



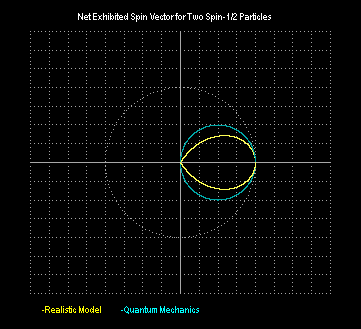
The quantum mechanical distribution is a perfect circle centered on
the point (1/2,0), whereas the simple realistic model gives a 
"teardrop" shaped distribution.  The density of the QM distribution 
is uniform as a function of q, with a 2:1 counter-rotating relationship 
as illustrated below

               |
               |                  2nd Measurement Angle
               |                 /
               |      *  *   /
               |   *     /  *
               | *   /        *
               |*/  q          *
           ----|---------------------  1st Measurement Angle
               |*    2q/       *1
               | *    /       *
               |   * /      *
               |    v *  *
               |   net
               |   spin vector


The density of the simple realistic model is given by counter-rotating
directions with an overall 2:1 ratio, but it is non-uniform over the
distribution.  Taking these respectively as the discrete "steps" for 
random walks, we can compare the long-term "positions", and the 
difference in positions, of these two distributions, for a given 
sequence of q and w values.  It would be interesting to know if
these two distributions of "steps" leads to significantly different
random walk characteristics.  I believe the mean step size is larger
for the simple realistic model, because it's distributed more heavily
on the outer rim, but the few numerical trials I've done haven't shown 
any noticeably greater tendancy for the realistic model to diverge.


As discussed above, the net exhibited spin resulting from measurements 
of two spin-1/2 particles taken along directions that differ by the 
angle q is
             S(q)  =  1  +  (2C(q) - 1) exp(iq)

where C(q) is the correlation (0 to 1) between the measurements.
We'll now show that the average magnitude of this vector (versus the 
angle q) is in fact slightly smaller if we assume the correlation 
function predicted by quantum mechanics than if we assume the linear 
correlation predicted by a simple realistic model.  

The average magnitude based on the QM correlation function is exactly 
2/pi = 0.636619... times the unit spin vector.  In comparison, the 
linear "realistic" correlation gives an average net spin of 0.65733... 
spin units, which is about 3% greater.  Therefore, the rate of divergence 
of net exhibited spin (based on a random walk with these step sizes) 
would be less based on the QM correlation.  This raises an interesting 
question:  Of all monotonic functions C(q) passing through the points 
(0,0), (pi/2,1/2) and (pi,1), which of them *minimizes* the exhibited 
spin divergence?  

Since the correlation is really just a function of the absolute 
value of q, it's clear that C is an "even" function, i.e., 
C(q) = C(-q).  The magnitude of the complex number S(q) is given 
by
           ___________      ________________________________________
 M(q)  =  / S(q) S(-q)  =  / 2(1-cos(q)) - 4(1-cos(q))C(q) + 4C(q)^2


Therefore, in summary, we want the function C(q) such that 

       C(0)=0       C(pi/2)=1/2      C(pi)=1     C(x)=C(-x)

and such that the mean of M(q), i.e., the integral

           pi
       1   /   ________________________________________
      ---  |  / 2(1-cos(q)) - 4(1-cos(q))C(q) + 4C(q)^2  dq
       pi  /
           0

is minimized.  If we denote the integrand by F(q,C,C') we can determine
the function C(q) that makes this integral stationary by the calculus 
of variations.  Euler's equation gives

               d  DF     DF
               -- --  -  --  =  0
               dq DC'    DC

where the D's signify partial derivatives.  Since DF/DC' = 0 we have

   DF       _             2C - (1-cos(q))
  ----  =  /2  ---------------------------------------  =  0
   DC          sqrt(1 - cos(q) - C2 + 2Ccos(q) + 2C^2)

Therefore, the unique correlation function for spin-1/2 particles that 
minimizes the divergence of exhibited spin is

                         1 - cos(q)
               C(q)  =  ------------
                             2

which is the quantum mechanical prediction for the correlation.

We've seen how the correlation between spin measurements of two 
spin-1/2 particles as a function of the relative angle of 
measurement can be derived from a certain variational principle.  
Specifically, the correlation function predicted by QM can be shown 
to minimize the mean step-size of the cumulative net spin vector 
exhibited by the particles over all possible relative angles of 
measurement.

More generally, it appears that this principle (minimizing the
net unconserved quantities over the range of possible interactions)
underlies all quantum mechanical processes.  Adapting Kant's term, 
we might describe this principle as the "categorical imperative",
i.e., each individual particle's exhibited behavior is governed 
by THE rule that would have to be followed by all such particles 
in equivalent circumstances in order to minimize the overall 
divergence in the evolution of the net "exhibited" quantities.

To see how this enters into the general quantum process, recall 
that in every measurement there is a degree of uncertainty 
depending on the precise manner in which the measurement is 
taken, i.e., the "basis" onto which we project the state vector 
to give the probabilities of the various possible discrete outcomes.  
The issue of conservation arises when we consider the interaction 
of two or more subsystems.  The crucial point is that we're free to 
select the bases for our measurements of these various subsystems 
independently, and therefore the bases are not, in general, 
parallel.  As a result, the exhibited behaviors of the subsystems 
will not, in general, be equal and opposite, and so each set of 
measurements represents a step in a random walk around the point 
of strict conservation.

We described this in detail for the case of quantum spin, where 
it was shown that the requirement to minimize the divergence from 
strict conservation of "exhibited spin" leads directly to the QM 
prediction for the correlation of spin measurements of coupled 
particles.  It seems to me now that this same argument can be used 
to derive the QM predictions for ALL quantum processes.

This seems interesting to me because it singles out - more or 
less from first principles - the pattern of behavior that yields 
the least divergent evolution of net exhibited quantities for any 
prescribed set of measurements.  This hypothetical pattern of 
behavior would be identifiable and significant as a limiting case 
even if we knew nothing about quantum mechanics.  Also, the fact 
that this evolution ultimately implies constraints on the supposedly 
free choices of measurement bases (as discussed above) is intriguing.  
In addition, the unavoidable evolution of net exhibited quantities, 
even in the context of a "conservative process", is suggestive of 
a fundamental temporal asymmetry that seems not to have been 
considered previously.