Bit-String Orbits Under Rotate-XOR
For any string of n binary bits we can arrange the bits in a circle,
and define the operation "rotate-xor" by exclusively-ORing each bit
with with corresponding bit of the circle rotated one place clockwise.
In other words, each bit is XOR'ed with it's predecessor in the loop.
Robert Sawyer called my attention to this operation, and pointed out
that the "flows" induced by iterating this operation on the finite
space of 2^n bit-strings are quite interesting. Indeed the structures
remind me very much of hydrocarbon molecules, because they tend to
cluster into closed loops, with inward-flowing branches attached to
the vertices of the eventual cycles. I wonder if some combinations
of atoms with the right valencies might tend to join according to
these XOR structures.
For n=3 there is just one cycle of period 3, and each vertex of
this cycle is fed by one other string. Also, we have the convergent
path from 7 to the fixed point 0. These two structures are shown
below.
With n=4 there are no non-trivial cycles, since every number flows
to the fixed point 0, as shown below.
The set of 5-bit strings has a single cycle of length 15, and each
vertex is fed by one other number. Also, the number 31 flows to the
fixed point 0, as illustrated below.
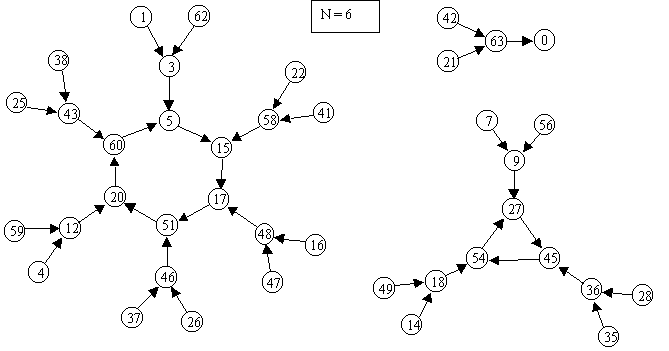
With n=6 we have two copies of the hexagonal structure shown below
on the left. The other copy (not shown) has all the numbers equal
to double the numbers in this figure modulo 63 (= 2^6 - 1). We also
have one triangular structure, as well as a single structure going
to the fixed point 0. Each vertex of these structures is fed by
a Y-shaped set of three numbers.
The set of 7-bit strings consists of nine septagonal structures as
shown in the figure below. Seven of these contains numbers that are
given by multiplying the numbers in the structure on the left below
by 2^k modulo 127 (= 2^7 - 1), for k=0,1,..,6. The other two
"articulated septagons" are are self-generated, i.e., multiplying
the numbers by 2^k (mod 127) gives rotated versions of themselves.
In general if n equals a power of 2 the resulting shift-xor structure
is a single binary tree flowing to the fixed point 0.
These "shift-XOR" structures are formally examples of what are called
"dynamic systems" (iteration patterns) produced by a particular unary
operation on the elements of a set. The cycles are the "attractors"
in these systems. Of course, as dynamic systems go, these shift-XOR
structures are not too complex, because the underlying field
(polynomials in Z_2[x] of degree n) is finite and necessarily leads
to strictly periodic sequences. Nevertheless, the resulting
structures are quite interesting. I think the wrap-around aspect
of the shift-XOR operation is what makes the results non-trivial.
Saywer asked for the number N(n) of distinct cycle-lengths as a
function of n, noting that he had empirically determined that
N(2) = N(4) = N(8) = N(16) = 1
N(3) = 2 N(5) = 2 N(6) = 3 N(7)=2
Also, he wondered what is the length L(n) of the longest cycle as a
function of n? He had found empirically that
L(2) = L(4) = L(8) = L(16) = 1
L(3) = 3 L(5) = 15 L(6) = 6 L(7) = 7
I think the answer to the first question follows immediately from
the answer to the second question. If L(n) = (2^t)(m) where m is
odd, then it appears that the number of distinct cycles lengths is
N(n) = t + 2 if m > 1, and N(n)=1 if m = 1. This is based on
the observation that if there is a cycle of length 2k > 1 then there
is also a cycle of length k, and conversely if there is a cycle of
length k < L(n) then there is a cycle of length 2k.
For example, the max cycle length for n=20 is 60, and there are also
cycles of length 30 and 15 (and of course 1). Thus L(20) = (2^2)(15)
and so t=2 and N(20) = t+2 = 4.
The second question is more difficult. It seems that if n=(2^k)m
where m is odd, then L(n) = 2^k L(m) if m>1, and L(n)=1 if m=1.
Also, it appears that L(n) is necessarily divisible by n, so we
only need to consider the values of L(n)/n. The values of L(n)/n
for the first few odd integers n are listed below
n L(n)/n L(n)
----- ------- -----
3 1 3
5 3 15
7 1 7
9 7 63
11 31 341 (1st pseudoprime to base 2)
13 63 819
15 1 15
17 15 255
19 511 9709
21 3 63
23 89 2047
25 1023 25575
27 511 13797
29 16383 475107
31 1 31
Notice that each L(n)/n is of the form 2^j - 1, with the exception
of n=23. However, in that case we have L(n) = 2047, which is of
this form. Also, in several other cases L(n) is of this form.
We might also notice that when n is of the form 2^j + 1 then it
appears L(n)/n is always n-2, as shown by the cases n = 3, 5,
9, 17. Also, when n is of the form 2^j - 1 it appears L(n)/n is
always 1, as shown by the cases n = 3, 7, 15, 31.
In general it seems that
2^[(n-1)/2) - j(n)] - 1
L(n)/n = ------------------------
d(n)
for some non-negative integer j(n) and positive integer d(n). The
values of these parameters for the first few odd n are shown below:
n j(n) d(n)
---- ----- -------
3 0 1
5 0 1
7 3 1 or (0 7)
9 0 1
11 0 1
13 0 1
15 7 1
17 4 1 or (0 17)
19 0 1
21 8 1 or (0 341) or (2 85) or (4 21) or (6 5)
23 0 23
25 2 1
27 3 1
29 0 1
31 15 1
Another way of approaching this is to examine the sequence of rotate-
XOR values of k for k=0,1,2,...,2^n - 1. If we let A(k) denote the
rotate-XOR of k (for some fixed number of bits n) and let M = 2^n - 1,
then clearly we have A(k)=A(M-k) for all k. In other words, the
sequence is palindromic. Also, for k from 0 to 2^(n-1) (which gives
the rest of the sequence via the palidromic property) the values of
A(k) are always the sequence
0 3 6 5 12 15 10 9 24 27 30 29 20 23 18 17 ...
and so on. (This is for a left-rotation, whereas for a right-rotation
these are the values of A(2n), and the odd terms are another sequence
beginning with 2^(n-1) + 1 and somewhat similar differences.) If we
let D(k) = A(k) - A(k-1) denote the first differences of this sequence,
the values of D(k) for k=1,2,... are
3 3 -1 7 3 -5 -1 15 3 3 -1 -9 3 -5 -1 -31 ...
and so on. These differences are given by
D( 4k + 1) = 3 D( 4k + 3) = -1
D( 8k + 2) = 3 D( 8k + 6) = -5
D(16k + 4) = 7 D(16k + 12) = -9
D(32k + 8) = 15 D(32k + 24) = -17
: :
In general the positive differences for j greater than 1 are
D[(2^(j+1))k + 2^(j-1)] = 2^j - 1
and the negative differences are
D[(2^(j+1))k + 3(2^(j-1))] = -(2^j + 1)
So, to determine the value of A(N) for some given integer N we need
only count the number of integers of these various forms less than
or equal to N. For example, with N=18 we know the numbers of the
form 4k+1 less than or equal to 18 are
3 4k + 1 = 1, 5, 9, 13, 17
-1 4k + 3 = 3, 7, 11, 15
3 8k + 2 = 2, 10, 18
-5 8k + 6 = 6, 14
7 16k + 4 = 4
-9 16k + 12 = 12
15 32k + 8 = 8
-17 32k + 24 = -
31 64k + 16 = 16
Therefore we have
A(18) = 5(3) + 4(-1) + 3(3) + 2(-5) + 1(7)
+ 1(-9) + 1(15) + 0(-17) + 1(31)
= 54
Obviously the number of integers of the form mk+n less than or equal
to N is just 1 + {(N-n)/m} where {x} signifies the greatest non-
negative integer not exceeding x. Combining this with the preceding
expressions for D(k) gives a summation for A(n).
Notice that the first differences would be more consistent if the
lowest-order magnitudes were swapped, i.e., if the difference for
steps numbered 4k+1 was 1 and the difference for steps numbered
4k+3 was -3. This more consistent set of first-differences gives a
sequence a(k) that is closely related to A(k), as shown below
k: 0 1 2 3 4 5 6 7 8 ...
A(k): 0 3 6 5 12 15 10 9 24 ...
a(k): 0 1 4 1 8 9 4 1 16 ...
A-a: 0 2 2 4 4 6 6 8 8 ...
We see that A(k) = a(k) + k if k is even, and A(k) = a(k) + (k+1)
if k is odd. Also, we can express a(N) as the sum of the "consistent"
first differences
N
a(N) = SUM [ (s_k)*2^(t_k + 1) - 1 ]
k=1
where s_k equals +1 or -1 accordingly as the odd part of k is
congruent to 1 or 3 (mod 4), and t_k equals the power of 2 dividing
k. Thus, for even integers N we have
N
A(N) = 2 SUM (s_k) 2^t_k
k=1
and for odd integers N we have
N
A(N) = 1 + 2 SUM (s_k) 2^t_k
k=1
From more general considerations we can see that A(x) equals k then
A(x') also equals k, where x' is the bit-wise complement of x. For
example, considering six-bit strings, we see that both the numbers
x = 100110 (38)
x' = 011001 (25)
flow to 101011 (43) under the rotate-XOR operation. Furthermore,
this pair of numbers is unique, i.e., there can be no other numbers
y such that A(y)=43. To see this, we can directly determine the
complementary pair (x,x') that flow to any given number as indicated
below
101011 (43)
x 0
------
L(x) 1
Here we have arbitrarily taken the least significant bit of x as
zero (which can can certainly do by exchanging x and x'), and we
can infer the least significant bit of the left-rotation of x,
denoted by L(x), by the reciprocity of the exclusive OR. Also,
we know the next bit of L(x) is the left-shifted least bit of x,
so we can bring that 0 down to L(x), and use it to infer the next
bit of x, as follows
101011 (43)
x 10
------
L(x) 01
Now we can bring this new bit of x down and to the left one place
in L(x), and use it to infer the next bit of x
101011 (43)
x 110
------
L(x) 101
and so on. When we have completed this process we have the result
101011 (43)
x 100110 (38)
------
L(x) 001101
Of course if we have started with a 1 as the least bit of x, we would
have generated the complement x' = 011001 (25).
Likewise for any k we can determine the unique pair of integers that
flow to k, if any such exist. (The number zero flows to itself, and
it's complement 2^n - 1 also flows to zero.) Exactly half of all the
numbers (for any fixed binary length) have "predecessors" in this
sense. The others do not yield a consistent result to the above
procedure when we try to wrap the last bit around.
In general, for n-bit strings, if we set n = m 2^t for some odd
integer m, then every vertex of a cycle (as well as the number 0,
which is periodic with period 1) is fed by a binary tree with 2^t
layers. Thus, if n is odd, as in the cases n=3, 5, or 7 illustrated
above, each vertex is fed by a single "external" number with no
predecessors. On the other hand, with n=6 = 3*2^1 each vertex is
fed by a binary tree with 2 levels. Also, with n = 4 = 2^2, each
vertex (which is just zero in this case) is fed by a 4-layer binary
tree.
Also, if d divides n, then the structures of n-bit numbers include
copies of the d-bit structures with each number multiplied by
(2^n - 1)/(2^d - 1) (mod 2^n - 1), plus the appropriate size of
binary tree into each vertex. For example, with n=3 we had the
simple triangular cycle (3,5,6) with each vertex fed by a single
number. Since 6 is divisible by 3, we know that there must be a
triangular structure with 6-bit strings, with the numbers multiplied
by (2^6 - 1)/(2^3 - 1) = 63/7 = 9 modulo 63. Indeed as we saw
previously the 6-bit strings include a triangular cycle with the
numbers (27,45,54), with each vertex fed by a two-level binary
tree (because 6 is divisible by 2).
With these understandings we can infer the structures for larger
values of n, based solely on the numbers of cycles of various lengths.
Here is a brief table
cycle cycle
n length number n length number
--- ------ ------ --- ------ ------
9 63 4 15 15 1091
3 1 5 3
1 1 3 1
1 1
10 30 8
15 1 16 - none
1 1
17 255 256
11 341 3 85 3
1 1 1 1
12 12 20 18
6 2
3 1
1 1 19 9709 27
1 1
13 819 5
1 1
14 14 288
7 9
1 1
The number of vertices is just the sum of products of cycles and
lengths, and if we multiply each of these by 2^(2^t) where 2^t is
the even part of n we get the total number of n-bit strings, which
of course is 2^n. For example, each vertex of an n=12 structure is
the base of a binary tree of 4 levels (because 4 is the highest power
of 2 dividing 12), so each vertex implies 2^4 = 16 numbers. Thus
in total we have
20 *12 = 240
2 * 6 = 12
1 * 3 = 3
1 * 1 = 1
---
256 * 16 = 4096 = 2^12
We can characterize each cycle by its smallest term, and then easily
generate the remaining terms, noting that the left-rotation of x is
given by 2x modulo 2^n - 1 (unless x = 2^n - 1, in which case the
left-rotation is simply 0).
Return to MathPages Main Menu
Сайт управляется системой
uCoz