 Archimedes on Spheres and Cylinders
Archimedes on Spheres and Cylinders
Archimedes was killed during the massacre that followed the capture
of Syracuse by the Roman general Marcellus in 212 BC, even though
Marcellus had given orders that the renowned sage (who was then in
his 75th year) was not to be harmed. According to one story, in the
midst of the general mayhem a Roman soldier came upon an old man
drawing diagrams in the sand, and ran him through. Marcellus was
distraught at the news, and saw to it that Archimedes was given a
burial in accordance with his wishes, including a monument featuring
a stone sphere and cylinder. This had been Archimedes' wish, because
he regarded his discoveries on the volumes and surface areas of these
solids as his most important - and most beautiful - achievements.
Alas, during the century that followed, this monument to one of
history's greatest scientists fell into neglect and was forgotten.
Cicero (106-43 BC), the great Roman statesman and orator, learned
as a boy about Archimedes, and later used the mathematician's life as
an example of "a good life", in contrast with another Sryacusan, the
tyrant Dionysius, who achieved supreme power, but became a prisoner
of his own brutal regime and the requirements of maintaining his
power. Coincidentally, Cicero's first public office (in 75 BC) was
to serve as a quaestor (Roman administrator) in Sicily. In Book V
of his "Tusculanarum Disputationum" Cicero digresses in the midst of
discoursing on the futility of Dionysius' existence by recounting an
interesting episode:
When I was quaestor in Sicily I managed to track down
Archimedes' grave. The Syracusans knew nothing about
it, and indeed denied that any such thing existed. But
there it was, completely surrounded and hidden by bushes
of brambles and thorns. I remembered having heard of
some simple lines of verse which had been inscribed on
his tomb, referring to a sphere and cylinder modelled in
stone on top of the grave. And so I took a good look
round all the numerous tombs that stand beside the
Agrigentine Gate.
Finally I noticed a little column, just visible above the
scrub: it was surmounted by a sphere and a cylinder. I
immediately said to the Syracusans, some of whose leading
citizens were with me at the time, that I believed this
was the very object I had been looking for. Men were sent
in with sickles to clear the site, and when a path to the
monument had been opened we walked right up to it. And
the verses were still visible, though approximately the
second half of each line had been worn away.
So one of the most famous cities in the Greek world, and
in former days a great center of learning as well, would
have remained in total ignorance of the tomb of the most
brilliant citizen it had ever produced, had a man from
Arpinum not come and pointed it out!
But now to return to the point where I started that
digression. Surely anyone who has even the slightest
connexion with the Muses, that is to say with civilization
and learning, would rather be the mathematician Archimedes
than the tyrant Dionysius. If we weigh up the two men's
ways of life and behavior, we find that one of them fed
his brain on scientific research and discovery, with all
the satisfaction that comes with intense intellectual
exercise - which is the most wonderful spiritual
nourishment in the world - while the thoughts of the
other dwelt on murder and oppression, and fear was his
companion day and night. Compare Dionysius with
Democritus, Pythagoras, Anaxagoras. What thrones or
possessions on all the earth could you rank higher than
their philosophical achievements, and the satisfaction
they derived from them?
That's certainly a fine sentiment regarding the serene contemplation
of the universe, untroubled by the baser concerns of life, although
it's only fair to recall that both Archimedes and Pythagoras were
murdered, and Anaxagoras was imprisioned and sentenced to death for
some of his beliefs (e.g., that the Sun was a red-hot stone, and the
Moon was made of "earth"). Anyway, the tomb of Archimedes subsequently
fell into neglect again, and presumably (?) no longer exists.
Why was Archimedes so fond of the sphere and the cylinder? To answer
this, we should back up a little, and consider the circle. The number
pi is defined as the ratio of the circumference to the diameter of a
circle, so for any circle we have C = 2 pi r, by definition. But what
is the area of a circle? Is it necessary to define a new number to
express this area in terms of the linear dimensions of the circle?
Archimedes approached this question very cleverly, realizing that he
could easily establish upper and lower bounds on the area of a
circle in terms of the circumference and the radius, and then show
that those bounds can be made to converge arbitrarily close to each
other, leaving only one possibility for the area of a circle.
To establish a lower bound on the area of a circle of radius r,
suppose we inscribe a regular n-sided polygon within the circle.
Notice that this polygon can be decomposed into n identical triangular
slices meeting at the center of the circle, as illustrated below for
the case n=6.
 The outer edges of these triangles approximate the circumference of
the circle. Also, defined a straight line as the shortest path
connecting two given points, so the sum of these n linear segments
is necessarily (slightly) less than the circumference. Also, the
"height" of these individual triangles (taking the outer edge as
the "base") is slightly less than the radius of the circle. However,
by increasing n, the sum of the outer edges can be made arbitrarily
close to the circumference C of the circle, and the "heights" of the
triangles can be made arbitrarily close to the radius r of the circle.
Also, since the area of each triangle is half its "height" times its
base, and the sum of their areas is half their height times the sum of
their bases, we see that it's possible to inscribe within the circle
a regular n-gon whose area is arbitrarily close to rC/2. It follows
that the area of the circle cannot be less than rC/2.
Similarly, by circumscribing a regular n-sided polygon around a circle,
as shown below for n=6, we can easily see that the area of the polygon
can be made arbitrarily close to rC/2.
The outer edges of these triangles approximate the circumference of
the circle. Also, defined a straight line as the shortest path
connecting two given points, so the sum of these n linear segments
is necessarily (slightly) less than the circumference. Also, the
"height" of these individual triangles (taking the outer edge as
the "base") is slightly less than the radius of the circle. However,
by increasing n, the sum of the outer edges can be made arbitrarily
close to the circumference C of the circle, and the "heights" of the
triangles can be made arbitrarily close to the radius r of the circle.
Also, since the area of each triangle is half its "height" times its
base, and the sum of their areas is half their height times the sum of
their bases, we see that it's possible to inscribe within the circle
a regular n-gon whose area is arbitrarily close to rC/2. It follows
that the area of the circle cannot be less than rC/2.
Similarly, by circumscribing a regular n-sided polygon around a circle,
as shown below for n=6, we can easily see that the area of the polygon
can be made arbitrarily close to rC/2.
 Therefore, the area of the circle cannot be greater than rC/2. So,
since the circle's area cannot be either less than or greater than
rC/2, it must be rC/2. This is the form of the argument as presented
by Archimedes. Of course, since C = 2 pi r, Archimedes' result is
equivalent to the modern formula A = pi r^2 for the area of a circle.
This establishes the fact that the number pi, which we originally
defined as the ratio of the circumference to the diameter of a circle,
is also the ratio of the circle's area to the area of a square whose
edges equal the circle's radius.
Now let's move on to the sphere. It's natural to ask what is the
surface area of a sphere, but Archimedes answered a more general
question, giving a recipe for the surface area of ANY section of a
sphere cut off by a plane. Specifically, he discovered and proved
that the surface area of a region of a sphere sliced off by a plane
equals the area of a circle whose radius is the straight-line distance
from the central point of that region to the perimeter.
To prove this, consider a sphere cut by a horizontal plane as shown
in the side view below.
Therefore, the area of the circle cannot be greater than rC/2. So,
since the circle's area cannot be either less than or greater than
rC/2, it must be rC/2. This is the form of the argument as presented
by Archimedes. Of course, since C = 2 pi r, Archimedes' result is
equivalent to the modern formula A = pi r^2 for the area of a circle.
This establishes the fact that the number pi, which we originally
defined as the ratio of the circumference to the diameter of a circle,
is also the ratio of the circle's area to the area of a square whose
edges equal the circle's radius.
Now let's move on to the sphere. It's natural to ask what is the
surface area of a sphere, but Archimedes answered a more general
question, giving a recipe for the surface area of ANY section of a
sphere cut off by a plane. Specifically, he discovered and proved
that the surface area of a region of a sphere sliced off by a plane
equals the area of a circle whose radius is the straight-line distance
from the central point of that region to the perimeter.
To prove this, consider a sphere cut by a horizontal plane as shown
in the side view below.
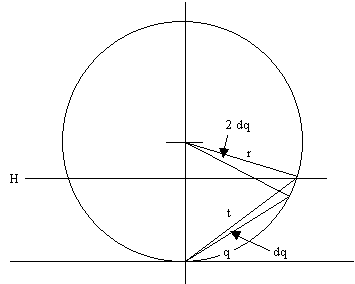 Archimedes' theorem is that the surface area of the region of the
sphere below the horizontal plane H is equal to the area of a circle
of radius t. This is obviously true if H is just tangent to the bottom
of the sphere, since in that case both areas are zero. Our approach
will be to show that an incremental change in the height of H (or,
equivalently, in the angle q) changes the two surface areas by the
same amount, so they are always equal.
Since we've already examined Archimedes' method of deducing results in
infintesimal reasoning by excluding all other possibilities, let's
take advantage of some trigonometry and calculus notation to simplify
the present derivation. Notice that the distance from the end of the
vector t to the center of the circle is r, so we have
[t cos(q)]^2 + [t sin(q) - r]^2 = r^2
This gives
t = 2r sin(q)
Now, using the formalism of calculus to sketch Archimedes' argument,
we can see that dt/dq = 2r cos(q), which is to say (informally) that
the incremental change dt in t for an incremental change dq in q is
dt = 2r cos(q) dq. We know from our earlier result that the area of
a circle of radius t is A = pi t^2, so the incremental change dA in
the area A corresponding to an incremental change dt in the length
of t is dA = 2pi t dt. Multiplying (dt/dq) and (dA/dt) gives dA/dq,
which can be written as
dA = 4pi rt cos(q) dq
which tells us how the area of a circle of radius t changes as we
change the angle q. Now, how does the surface area of the sphere
below the plane H change for the same change in q? Well, if the
vector t sweeps out an incremental angle dq, the radial vector r
sweeps out an angle 2 dq. (This is a nice elementary fact of
trigonometry, as discussed in Loci of Equi-angular Points. Also,
we know that the arc length swept out by an angular displacement
2 dq is equal to 2 dq r, so this is the width of the incremental
stripe on the surface of the sphere. The circumference of this
stripe is obviously 2pi t cos(q), so the incremental change in
surface area of the spherical region is the product of these, i.e.,
dA = 4pi rt cos(q) dq
which is exactly the same as the incremental change in the area of
a circle of radius t. Hence we have proved Archimedes' result.
In particular, suppose we raise the plane H so that it is tangent to
the TOP of the sphere. Archimedes' theorem then tells us that the
surface area of the entire sphere equals the area of a circle of
radius t = 2r, so we have A_sphere = pi (2r)^2 = 4 pi r^2. This is
one of the results that Archimedes' valued so highly, because it
shows that the surface area of a sphere is exactly 4 times the area
of a circle with the same radius. Of course, every school child knows
this today, but if we try to imagine a time when this was not known,
and then discovering it, we can appreciate that it is a truly
beautiful result.
But where is the cylinder in all of this? Well, you may notice that
the surface area around the circluar walls of a cylinder of radius r
and height 2r (i.e., a cylinder circumscribed on a sphere) is equal
to (2pi r)(2r) = 4pi r^2, the same as the surface area of the inscribed
sphere. Archimedes showed that not only are these total areas equal,
but the areas cut off by any planes perpendicular to the cylinder's
axis are also equal. In other words, the surface area of the sphere
over any vertical span is equal to the surface area of the
circumscribing cylinder over that same span. To see this, let's
look again at the side view of the sphere, this time inscribed in
a cylinder whose flat faces are tangent to the top and bottom of
the sphere, as shown below.
Archimedes' theorem is that the surface area of the region of the
sphere below the horizontal plane H is equal to the area of a circle
of radius t. This is obviously true if H is just tangent to the bottom
of the sphere, since in that case both areas are zero. Our approach
will be to show that an incremental change in the height of H (or,
equivalently, in the angle q) changes the two surface areas by the
same amount, so they are always equal.
Since we've already examined Archimedes' method of deducing results in
infintesimal reasoning by excluding all other possibilities, let's
take advantage of some trigonometry and calculus notation to simplify
the present derivation. Notice that the distance from the end of the
vector t to the center of the circle is r, so we have
[t cos(q)]^2 + [t sin(q) - r]^2 = r^2
This gives
t = 2r sin(q)
Now, using the formalism of calculus to sketch Archimedes' argument,
we can see that dt/dq = 2r cos(q), which is to say (informally) that
the incremental change dt in t for an incremental change dq in q is
dt = 2r cos(q) dq. We know from our earlier result that the area of
a circle of radius t is A = pi t^2, so the incremental change dA in
the area A corresponding to an incremental change dt in the length
of t is dA = 2pi t dt. Multiplying (dt/dq) and (dA/dt) gives dA/dq,
which can be written as
dA = 4pi rt cos(q) dq
which tells us how the area of a circle of radius t changes as we
change the angle q. Now, how does the surface area of the sphere
below the plane H change for the same change in q? Well, if the
vector t sweeps out an incremental angle dq, the radial vector r
sweeps out an angle 2 dq. (This is a nice elementary fact of
trigonometry, as discussed in Loci of Equi-angular Points. Also,
we know that the arc length swept out by an angular displacement
2 dq is equal to 2 dq r, so this is the width of the incremental
stripe on the surface of the sphere. The circumference of this
stripe is obviously 2pi t cos(q), so the incremental change in
surface area of the spherical region is the product of these, i.e.,
dA = 4pi rt cos(q) dq
which is exactly the same as the incremental change in the area of
a circle of radius t. Hence we have proved Archimedes' result.
In particular, suppose we raise the plane H so that it is tangent to
the TOP of the sphere. Archimedes' theorem then tells us that the
surface area of the entire sphere equals the area of a circle of
radius t = 2r, so we have A_sphere = pi (2r)^2 = 4 pi r^2. This is
one of the results that Archimedes' valued so highly, because it
shows that the surface area of a sphere is exactly 4 times the area
of a circle with the same radius. Of course, every school child knows
this today, but if we try to imagine a time when this was not known,
and then discovering it, we can appreciate that it is a truly
beautiful result.
But where is the cylinder in all of this? Well, you may notice that
the surface area around the circluar walls of a cylinder of radius r
and height 2r (i.e., a cylinder circumscribed on a sphere) is equal
to (2pi r)(2r) = 4pi r^2, the same as the surface area of the inscribed
sphere. Archimedes showed that not only are these total areas equal,
but the areas cut off by any planes perpendicular to the cylinder's
axis are also equal. In other words, the surface area of the sphere
over any vertical span is equal to the surface area of the
circumscribing cylinder over that same span. To see this, let's
look again at the side view of the sphere, this time inscribed in
a cylinder whose flat faces are tangent to the top and bottom of
the sphere, as shown below.
 The incremental surface area of the cylinder slice between the planes
A and B is 2pi r dy, and the surface area of the sphere between those
planes is 2pi x dc. Also, we see that the right triangle with edge
lengths x,y and hypotenuse r is similar to the right triangle with
edge lengths dy,dx and hypotenuse dc, so we have dc/dy = r/x, which
implies x dc = r dy, and so the surface areas of the sphere and the
cylinder between the planes A and B are equal over any vertical span.
This is another remarkable result.
Archimedes then went on to consider the VOLUME of the sphere. Before
we describe that, let's first recall one of the earliest mathematical
theorems concerning geometry, one that seems to have been known
(though perhaps only empirically) by the earliest Egyptians and
Babylonians, namely, that the volume of a right cone equals 1/3 the
volume of the circumscribing cylinder. More generally, the volume of
any right pyramid is 1/3 the volume of the prism on the same base
with the same height. Archimedes attributed the first clear statement
of this fact to Democritus, but said that the first truly scientific
proof was due to Eudoxus, who applied his "method of exhaustion".
How would we prove this with modern methods? If the area of the base
is A, and if we tip this solid upside down, the area on any horizontal
slice can be expressed as a function of the height h above the vertex
as A(h) = (A/H^2)h^2. Integrating this from h=0 to h=H gives (1/3)AH,
which is indeed 1/3 the volume of the circumscribing prism or cylinder.
On the other hand, we can deduce this same result without integration,
simply based on the fact that the volumes of similar solids are
proportional to the cube of their linear dimension, e.g. the volume
of a sphere is proportional to the cube of the radius (whis is
another result sometimes attributed to Eudoxus). Consider a right
pyramid on a square base, and pass a plane through this pyramid
parallel to its base at half the height. Then partition this solid
as shown below.
The incremental surface area of the cylinder slice between the planes
A and B is 2pi r dy, and the surface area of the sphere between those
planes is 2pi x dc. Also, we see that the right triangle with edge
lengths x,y and hypotenuse r is similar to the right triangle with
edge lengths dy,dx and hypotenuse dc, so we have dc/dy = r/x, which
implies x dc = r dy, and so the surface areas of the sphere and the
cylinder between the planes A and B are equal over any vertical span.
This is another remarkable result.
Archimedes then went on to consider the VOLUME of the sphere. Before
we describe that, let's first recall one of the earliest mathematical
theorems concerning geometry, one that seems to have been known
(though perhaps only empirically) by the earliest Egyptians and
Babylonians, namely, that the volume of a right cone equals 1/3 the
volume of the circumscribing cylinder. More generally, the volume of
any right pyramid is 1/3 the volume of the prism on the same base
with the same height. Archimedes attributed the first clear statement
of this fact to Democritus, but said that the first truly scientific
proof was due to Eudoxus, who applied his "method of exhaustion".
How would we prove this with modern methods? If the area of the base
is A, and if we tip this solid upside down, the area on any horizontal
slice can be expressed as a function of the height h above the vertex
as A(h) = (A/H^2)h^2. Integrating this from h=0 to h=H gives (1/3)AH,
which is indeed 1/3 the volume of the circumscribing prism or cylinder.
On the other hand, we can deduce this same result without integration,
simply based on the fact that the volumes of similar solids are
proportional to the cube of their linear dimension, e.g. the volume
of a sphere is proportional to the cube of the radius (whis is
another result sometimes attributed to Eudoxus). Consider a right
pyramid on a square base, and pass a plane through this pyramid
parallel to its base at half the height. Then partition this solid
as shown below.
 We see that the pyramid is comprised of six equal sub-pyramids (one of
them upside down), each similar to and half the height of the original,
plus four copies of a tetrahedral solid typified by the one outlined
in red. Now, we know that the volume of each sub-pyramid is 1/8 the
volume of the total pyramid (since the cube of 1/2 is 1/8). Hence
these sub-pyramids take up 3/4 of the original pyramid, leaving 1/4
to be taken up by the four identical tetrahedral solids. Therefore,
each of those has 1/16 of the total pyramid's volume, which is 1/2
of the volume of a sub-pyramid.
Now drop perpendiculars from the base corners of the upper sub-pyramid
to the base of the main pyramid, which gives the prism circumscribing
the upside-down sub-pyramid shown in yellow below.
We see that the pyramid is comprised of six equal sub-pyramids (one of
them upside down), each similar to and half the height of the original,
plus four copies of a tetrahedral solid typified by the one outlined
in red. Now, we know that the volume of each sub-pyramid is 1/8 the
volume of the total pyramid (since the cube of 1/2 is 1/8). Hence
these sub-pyramids take up 3/4 of the original pyramid, leaving 1/4
to be taken up by the four identical tetrahedral solids. Therefore,
each of those has 1/16 of the total pyramid's volume, which is 1/2
of the volume of a sub-pyramid.
Now drop perpendiculars from the base corners of the upper sub-pyramid
to the base of the main pyramid, which gives the prism circumscribing
the upside-down sub-pyramid shown in yellow below.
 In addition to containing the upside-down sub-pyramid, this prism also
contains 1/4 of each of the four lower sub-pyramids, and 1/2 of each
of the four tetrahedral solids. Together, these extra pieces represent
the volume of two full sub-pyramids, to the entire yellow prism has
a volume equal to three times the volume of the inscribed pyramid.
Consequently, by similarity, each pyramid's volume is exactly 1/3 the
circumscribing prism.
It might seem that this visual approach is only applicable to the
special case of a right pyramid on a square base, but we immediately
see that if we stand such a pyramid next to any prism and pyramid,
or cylinder and cone, of the same height, and pass horizontal planes
through both solids parallel to the common plane of their bases,
then the areas of the of the circumscribing and interior solids,
respectively, are always in constant proportion, so this suffices
to prove that ANY linearly tapering pointed solid on an arbitrary
base has 1/3 the volume of the prism on the same base with the same
height.
Incidentally, this same partition of the pryamid enables us to
determine that the average height of the points of this solid is
exactly 1/4 the height of the pyramid itself. If the average height
of the points of a pyramid of height H is kH for some constant k,
then we have
4 / H \ 1 / H H \ 1 / H H \ 2 / 1 H \
kH = - ( k - ) + - ( - - k - ) + - ( - + k - ) + - ( - - )
8 \ 2 / 8 \ 2 2 / 8 \ 2 2 / 8 \ 2 2 /
/ k 3 \
= ( - + -- ) H
\ 4 16 /
from which we get k = 1/4. (This is another example of the kind of
technique discussed in the note Why Calculus?.)
Finally, let's consider the volume of the sphere. Once again
Archimedes found that we can express this quantity as a simple rational
multiple of the transcendental number pi. The area of the circular
slice of a sphere of radius R cut by a plane at a distance y above
the equatorial plane is A = pi x^2 where x^2 + y^2 = R^2. Hence
it's trivial using modern integration to compute the volume of the
sphere as follows
R
/ 4
V = pi | (R^2 - y^2) dy = - pi R^3
/ 3
y=-R
Since the volume of the circumscribing cylinder is obviously 2pi R^3,
we have Archimedes' result that the sphere has 2/3 the volume of the
circumscribing cylinder. Interestingly, if we include the two flat
ends of the cylinder, it's surface area is 6pi R^2, so the sphere's
surface area is 2/3 the total surface area of the circumscribing
cylinder. This delighted Archimedes, to have shown that both the
volume and the surface area of a sphere is 2/3 that of the
circumscribing cylinder.
To conclude, it's interesting to see how the ingenious methods of
Archimedes can sometimes gives results that bypass some fairly
elaborate calculus. To illustrate, consider how one would determine
the volume removed from a steel cylinder of radius R when a round hole
of radius R is drilled through it, perpendicular to the cylinder's
length. It's important that the hole's diameter is the same as the
cylinder's, because otherwise the answer is an elliptic integral that
usually won't be expressible in any "nice" form.
Anyway, given that the radius of the cylinder and the radius of the
hole are both R, we can cut the cylinder in half by a plane containing
its axis, and then set up orthogonal coordinates x,y in the plane
and z normal to the plane. Drill the hole along the z axis through
the origin. The volume removed is just (twice) the integral of the
cylinder's height above the plane, evaluated over the hole's circular
"footprint" on the plane. We really only need to evaluate 1 quadrant
of the footprint, because they are symmetrical. Thus, the answer is
given by the double integral
_________
R /R^2 - x^2
/ / __________
8 | | / R^2 - y^2 dy dx
/ /
x=0 y=0
which happens to work out nicely to (16/3)R^3.
But there's a more clever way of solving this problem. Imagine two
cylinders of equal radius intersecting each other at right angles.
Our problem is to find the volume of intersection. Now imagine a
sphere inscribed inside both cylinders, so it is inside the
intersection. If we slice off along a plane surface parallel to
both of the cylinder axes, the intersection of the cylinders will
be represented by a square region on this plane, and the sphere will
be a circular region. Also, it's not hard to see that the circular
region will always be inscribed in the square region, i.e., the
edges of the square will be tangent to the circle (because the
sphere touches each cylinder at every "height"). Therefore, at
every height the slice of area in the cylinder intersection is
4/pi time the area of the slice of the sphere, so the total volume
of the region of intersection is 4/pi times the volume of the
sphere, which is (4/pi)(4/3)pi R^3 = (16/3)R^3, in agreement with
what we found previously.
In addition to containing the upside-down sub-pyramid, this prism also
contains 1/4 of each of the four lower sub-pyramids, and 1/2 of each
of the four tetrahedral solids. Together, these extra pieces represent
the volume of two full sub-pyramids, to the entire yellow prism has
a volume equal to three times the volume of the inscribed pyramid.
Consequently, by similarity, each pyramid's volume is exactly 1/3 the
circumscribing prism.
It might seem that this visual approach is only applicable to the
special case of a right pyramid on a square base, but we immediately
see that if we stand such a pyramid next to any prism and pyramid,
or cylinder and cone, of the same height, and pass horizontal planes
through both solids parallel to the common plane of their bases,
then the areas of the of the circumscribing and interior solids,
respectively, are always in constant proportion, so this suffices
to prove that ANY linearly tapering pointed solid on an arbitrary
base has 1/3 the volume of the prism on the same base with the same
height.
Incidentally, this same partition of the pryamid enables us to
determine that the average height of the points of this solid is
exactly 1/4 the height of the pyramid itself. If the average height
of the points of a pyramid of height H is kH for some constant k,
then we have
4 / H \ 1 / H H \ 1 / H H \ 2 / 1 H \
kH = - ( k - ) + - ( - - k - ) + - ( - + k - ) + - ( - - )
8 \ 2 / 8 \ 2 2 / 8 \ 2 2 / 8 \ 2 2 /
/ k 3 \
= ( - + -- ) H
\ 4 16 /
from which we get k = 1/4. (This is another example of the kind of
technique discussed in the note Why Calculus?.)
Finally, let's consider the volume of the sphere. Once again
Archimedes found that we can express this quantity as a simple rational
multiple of the transcendental number pi. The area of the circular
slice of a sphere of radius R cut by a plane at a distance y above
the equatorial plane is A = pi x^2 where x^2 + y^2 = R^2. Hence
it's trivial using modern integration to compute the volume of the
sphere as follows
R
/ 4
V = pi | (R^2 - y^2) dy = - pi R^3
/ 3
y=-R
Since the volume of the circumscribing cylinder is obviously 2pi R^3,
we have Archimedes' result that the sphere has 2/3 the volume of the
circumscribing cylinder. Interestingly, if we include the two flat
ends of the cylinder, it's surface area is 6pi R^2, so the sphere's
surface area is 2/3 the total surface area of the circumscribing
cylinder. This delighted Archimedes, to have shown that both the
volume and the surface area of a sphere is 2/3 that of the
circumscribing cylinder.
To conclude, it's interesting to see how the ingenious methods of
Archimedes can sometimes gives results that bypass some fairly
elaborate calculus. To illustrate, consider how one would determine
the volume removed from a steel cylinder of radius R when a round hole
of radius R is drilled through it, perpendicular to the cylinder's
length. It's important that the hole's diameter is the same as the
cylinder's, because otherwise the answer is an elliptic integral that
usually won't be expressible in any "nice" form.
Anyway, given that the radius of the cylinder and the radius of the
hole are both R, we can cut the cylinder in half by a plane containing
its axis, and then set up orthogonal coordinates x,y in the plane
and z normal to the plane. Drill the hole along the z axis through
the origin. The volume removed is just (twice) the integral of the
cylinder's height above the plane, evaluated over the hole's circular
"footprint" on the plane. We really only need to evaluate 1 quadrant
of the footprint, because they are symmetrical. Thus, the answer is
given by the double integral
_________
R /R^2 - x^2
/ / __________
8 | | / R^2 - y^2 dy dx
/ /
x=0 y=0
which happens to work out nicely to (16/3)R^3.
But there's a more clever way of solving this problem. Imagine two
cylinders of equal radius intersecting each other at right angles.
Our problem is to find the volume of intersection. Now imagine a
sphere inscribed inside both cylinders, so it is inside the
intersection. If we slice off along a plane surface parallel to
both of the cylinder axes, the intersection of the cylinders will
be represented by a square region on this plane, and the sphere will
be a circular region. Also, it's not hard to see that the circular
region will always be inscribed in the square region, i.e., the
edges of the square will be tangent to the circle (because the
sphere touches each cylinder at every "height"). Therefore, at
every height the slice of area in the cylinder intersection is
4/pi time the area of the slice of the sphere, so the total volume
of the region of intersection is 4/pi times the volume of the
sphere, which is (4/pi)(4/3)pi R^3 = (16/3)R^3, in agreement with
what we found previously.
Return to MathPages Main Menu
Сайт управляется системой
uCoz Archimedes on Spheres and Cylinders
Archimedes on Spheres and Cylinders Archimedes on Spheres and Cylinders
Archimedes on Spheres and CylindersThe outer edges of these triangles approximate the circumference of the circle. Also, defined a straight line as the shortest path connecting two given points, so the sum of these n linear segments is necessarily (slightly) less than the circumference. Also, the "height" of these individual triangles (taking the outer edge as the "base") is slightly less than the radius of the circle. However, by increasing n, the sum of the outer edges can be made arbitrarily close to the circumference C of the circle, and the "heights" of the triangles can be made arbitrarily close to the radius r of the circle. Also, since the area of each triangle is half its "height" times its base, and the sum of their areas is half their height times the sum of their bases, we see that it's possible to inscribe within the circle a regular n-gon whose area is arbitrarily close to rC/2. It follows that the area of the circle cannot be less than rC/2. Similarly, by circumscribing a regular n-sided polygon around a circle, as shown below for n=6, we can easily see that the area of the polygon can be made arbitrarily close to rC/2.
Therefore, the area of the circle cannot be greater than rC/2. So, since the circle's area cannot be either less than or greater than rC/2, it must be rC/2. This is the form of the argument as presented by Archimedes. Of course, since C = 2 pi r, Archimedes' result is equivalent to the modern formula A = pi r^2 for the area of a circle. This establishes the fact that the number pi, which we originally defined as the ratio of the circumference to the diameter of a circle, is also the ratio of the circle's area to the area of a square whose edges equal the circle's radius. Now let's move on to the sphere. It's natural to ask what is the surface area of a sphere, but Archimedes answered a more general question, giving a recipe for the surface area of ANY section of a sphere cut off by a plane. Specifically, he discovered and proved that the surface area of a region of a sphere sliced off by a plane equals the area of a circle whose radius is the straight-line distance from the central point of that region to the perimeter. To prove this, consider a sphere cut by a horizontal plane as shown in the side view below.
Archimedes' theorem is that the surface area of the region of the sphere below the horizontal plane H is equal to the area of a circle of radius t. This is obviously true if H is just tangent to the bottom of the sphere, since in that case both areas are zero. Our approach will be to show that an incremental change in the height of H (or, equivalently, in the angle q) changes the two surface areas by the same amount, so they are always equal. Since we've already examined Archimedes' method of deducing results in infintesimal reasoning by excluding all other possibilities, let's take advantage of some trigonometry and calculus notation to simplify the present derivation. Notice that the distance from the end of the vector t to the center of the circle is r, so we have [t cos(q)]^2 + [t sin(q) - r]^2 = r^2 This gives t = 2r sin(q) Now, using the formalism of calculus to sketch Archimedes' argument, we can see that dt/dq = 2r cos(q), which is to say (informally) that the incremental change dt in t for an incremental change dq in q is dt = 2r cos(q) dq. We know from our earlier result that the area of a circle of radius t is A = pi t^2, so the incremental change dA in the area A corresponding to an incremental change dt in the length of t is dA = 2pi t dt. Multiplying (dt/dq) and (dA/dt) gives dA/dq, which can be written as dA = 4pi rt cos(q) dq which tells us how the area of a circle of radius t changes as we change the angle q. Now, how does the surface area of the sphere below the plane H change for the same change in q? Well, if the vector t sweeps out an incremental angle dq, the radial vector r sweeps out an angle 2 dq. (This is a nice elementary fact of trigonometry, as discussed in Loci of Equi-angular Points. Also, we know that the arc length swept out by an angular displacement 2 dq is equal to 2 dq r, so this is the width of the incremental stripe on the surface of the sphere. The circumference of this stripe is obviously 2pi t cos(q), so the incremental change in surface area of the spherical region is the product of these, i.e., dA = 4pi rt cos(q) dq which is exactly the same as the incremental change in the area of a circle of radius t. Hence we have proved Archimedes' result. In particular, suppose we raise the plane H so that it is tangent to the TOP of the sphere. Archimedes' theorem then tells us that the surface area of the entire sphere equals the area of a circle of radius t = 2r, so we have A_sphere = pi (2r)^2 = 4 pi r^2. This is one of the results that Archimedes' valued so highly, because it shows that the surface area of a sphere is exactly 4 times the area of a circle with the same radius. Of course, every school child knows this today, but if we try to imagine a time when this was not known, and then discovering it, we can appreciate that it is a truly beautiful result. But where is the cylinder in all of this? Well, you may notice that the surface area around the circluar walls of a cylinder of radius r and height 2r (i.e., a cylinder circumscribed on a sphere) is equal to (2pi r)(2r) = 4pi r^2, the same as the surface area of the inscribed sphere. Archimedes showed that not only are these total areas equal, but the areas cut off by any planes perpendicular to the cylinder's axis are also equal. In other words, the surface area of the sphere over any vertical span is equal to the surface area of the circumscribing cylinder over that same span. To see this, let's look again at the side view of the sphere, this time inscribed in a cylinder whose flat faces are tangent to the top and bottom of the sphere, as shown below.
The incremental surface area of the cylinder slice between the planes A and B is 2pi r dy, and the surface area of the sphere between those planes is 2pi x dc. Also, we see that the right triangle with edge lengths x,y and hypotenuse r is similar to the right triangle with edge lengths dy,dx and hypotenuse dc, so we have dc/dy = r/x, which implies x dc = r dy, and so the surface areas of the sphere and the cylinder between the planes A and B are equal over any vertical span. This is another remarkable result. Archimedes then went on to consider the VOLUME of the sphere. Before we describe that, let's first recall one of the earliest mathematical theorems concerning geometry, one that seems to have been known (though perhaps only empirically) by the earliest Egyptians and Babylonians, namely, that the volume of a right cone equals 1/3 the volume of the circumscribing cylinder. More generally, the volume of any right pyramid is 1/3 the volume of the prism on the same base with the same height. Archimedes attributed the first clear statement of this fact to Democritus, but said that the first truly scientific proof was due to Eudoxus, who applied his "method of exhaustion". How would we prove this with modern methods? If the area of the base is A, and if we tip this solid upside down, the area on any horizontal slice can be expressed as a function of the height h above the vertex as A(h) = (A/H^2)h^2. Integrating this from h=0 to h=H gives (1/3)AH, which is indeed 1/3 the volume of the circumscribing prism or cylinder. On the other hand, we can deduce this same result without integration, simply based on the fact that the volumes of similar solids are proportional to the cube of their linear dimension, e.g. the volume of a sphere is proportional to the cube of the radius (whis is another result sometimes attributed to Eudoxus). Consider a right pyramid on a square base, and pass a plane through this pyramid parallel to its base at half the height. Then partition this solid as shown below.
We see that the pyramid is comprised of six equal sub-pyramids (one of them upside down), each similar to and half the height of the original, plus four copies of a tetrahedral solid typified by the one outlined in red. Now, we know that the volume of each sub-pyramid is 1/8 the volume of the total pyramid (since the cube of 1/2 is 1/8). Hence these sub-pyramids take up 3/4 of the original pyramid, leaving 1/4 to be taken up by the four identical tetrahedral solids. Therefore, each of those has 1/16 of the total pyramid's volume, which is 1/2 of the volume of a sub-pyramid. Now drop perpendiculars from the base corners of the upper sub-pyramid to the base of the main pyramid, which gives the prism circumscribing the upside-down sub-pyramid shown in yellow below.
In addition to containing the upside-down sub-pyramid, this prism also contains 1/4 of each of the four lower sub-pyramids, and 1/2 of each of the four tetrahedral solids. Together, these extra pieces represent the volume of two full sub-pyramids, to the entire yellow prism has a volume equal to three times the volume of the inscribed pyramid. Consequently, by similarity, each pyramid's volume is exactly 1/3 the circumscribing prism. It might seem that this visual approach is only applicable to the special case of a right pyramid on a square base, but we immediately see that if we stand such a pyramid next to any prism and pyramid, or cylinder and cone, of the same height, and pass horizontal planes through both solids parallel to the common plane of their bases, then the areas of the of the circumscribing and interior solids, respectively, are always in constant proportion, so this suffices to prove that ANY linearly tapering pointed solid on an arbitrary base has 1/3 the volume of the prism on the same base with the same height. Incidentally, this same partition of the pryamid enables us to determine that the average height of the points of this solid is exactly 1/4 the height of the pyramid itself. If the average height of the points of a pyramid of height H is kH for some constant k, then we have 4 / H \ 1 / H H \ 1 / H H \ 2 / 1 H \ kH = - ( k - ) + - ( - - k - ) + - ( - + k - ) + - ( - - ) 8 \ 2 / 8 \ 2 2 / 8 \ 2 2 / 8 \ 2 2 / / k 3 \ = ( - + -- ) H \ 4 16 / from which we get k = 1/4. (This is another example of the kind of technique discussed in the note Why Calculus?.) Finally, let's consider the volume of the sphere. Once again Archimedes found that we can express this quantity as a simple rational multiple of the transcendental number pi. The area of the circular slice of a sphere of radius R cut by a plane at a distance y above the equatorial plane is A = pi x^2 where x^2 + y^2 = R^2. Hence it's trivial using modern integration to compute the volume of the sphere as follows R / 4 V = pi | (R^2 - y^2) dy = - pi R^3 / 3 y=-R Since the volume of the circumscribing cylinder is obviously 2pi R^3, we have Archimedes' result that the sphere has 2/3 the volume of the circumscribing cylinder. Interestingly, if we include the two flat ends of the cylinder, it's surface area is 6pi R^2, so the sphere's surface area is 2/3 the total surface area of the circumscribing cylinder. This delighted Archimedes, to have shown that both the volume and the surface area of a sphere is 2/3 that of the circumscribing cylinder. To conclude, it's interesting to see how the ingenious methods of Archimedes can sometimes gives results that bypass some fairly elaborate calculus. To illustrate, consider how one would determine the volume removed from a steel cylinder of radius R when a round hole of radius R is drilled through it, perpendicular to the cylinder's length. It's important that the hole's diameter is the same as the cylinder's, because otherwise the answer is an elliptic integral that usually won't be expressible in any "nice" form. Anyway, given that the radius of the cylinder and the radius of the hole are both R, we can cut the cylinder in half by a plane containing its axis, and then set up orthogonal coordinates x,y in the plane and z normal to the plane. Drill the hole along the z axis through the origin. The volume removed is just (twice) the integral of the cylinder's height above the plane, evaluated over the hole's circular "footprint" on the plane. We really only need to evaluate 1 quadrant of the footprint, because they are symmetrical. Thus, the answer is given by the double integral _________ R /R^2 - x^2 / / __________ 8 | | / R^2 - y^2 dy dx / / x=0 y=0 which happens to work out nicely to (16/3)R^3. But there's a more clever way of solving this problem. Imagine two cylinders of equal radius intersecting each other at right angles. Our problem is to find the volume of intersection. Now imagine a sphere inscribed inside both cylinders, so it is inside the intersection. If we slice off along a plane surface parallel to both of the cylinder axes, the intersection of the cylinders will be represented by a square region on this plane, and the sphere will be a circular region. Also, it's not hard to see that the circular region will always be inscribed in the square region, i.e., the edges of the square will be tangent to the circle (because the sphere touches each cylinder at every "height"). Therefore, at every height the slice of area in the cylinder intersection is 4/pi time the area of the slice of the sphere, so the total volume of the region of intersection is 4/pi times the volume of the sphere, which is (4/pi)(4/3)pi R^3 = (16/3)R^3, in agreement with what we found previously.