Rolling Spheres and Cones
Consider a sphere of unit radius rolling (at a constant rate, without
slipping or spinning) clockwise around a circle of radius R on a flat
plane. For what values of R will the sphere periodically be returned
to its initial configuration (position and orientation)? We can show
that the sphere's configuration will be periodic if and only if
R = sqrt(q^2-1) where q is a rational number greater than 1. Also,
q is the ratio of the plane circle's circumference to the circumference
of the circular locus of contact points on the sphere. Thus, if q=m/n
the sphere will resume its initial configuration every n times around
the circle.
As an example, setting q = 13/7, we find that a unit sphere rolling
around a plane circle of radius 2sqrt(30)/7 = 1.56492... will
return to its initial configuration every 7 times around the circle.
Obviously the smallest circle that has a period of 1 (i.e., for which
the sphere's configuration repeats with each trip around the circle)
has a radius of sqrt(3) = 1.73205..., whereas the smallest circle with
a period of 2 has a radius of sqrt(5)/2 = 1.11803... In general, the
smallest circle with period n has radius sqrt(2n+1)/n.
The equation R = sqrt(q^2 - 1) can be derived very simply if we
recognize that the pure rolling motion of a sphere in a circular
path on the plane is identical to the motion of a sphere inscribed
in a cone rolling on the plane, as illustrated below.
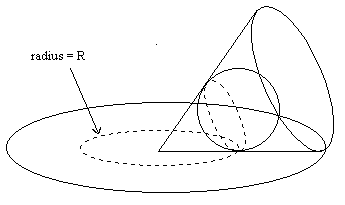 The circular locus of contact points is just the points of tangency
between the sphere and the cone, and the relations between R and the
circumference of that contact circle can be inferred directly from
the diagram. Incidentally, this shows that for a "right" cone - which
means the sphere and the plane circle have the same radius - the ratio
of contact circumferences is q = sqrt(1+1^2) = sqrt(2), so the sphere
will never return precisely to its initial configuration.
Now consider an arbitrary curve drawn on a flat surface, and a sphere
rolling (without slipping or spinning) along this curve. We can
parameterize the curve by giving the tangent angle "a" (relative to
an arbitrarily chosen axis) as a function of the distance along the
curve. If the sphere rolls along a straight line with angle "a" for
a finite distance L, the change in the orientation of the sphere is
given by multiplying the initial orientation by the rotation matrix
_ _
| ccC+ss cs(1-C) -cS |
M = | cs(1-C) ssC+cc sS | (1)
|_ cS -sS C _|
where c=cos(a), s=sin(a), C=cos(L/r), and S=sin(L/r) and r is the
radius of the sphere.
The net change in orientation after the sphere has rolled along k
linear segments, each of length L with the path angles a1, a2,...ak,
is given by the matrix product
M(net) = M(a1) M(a2) .... M(ak) (2)
As L approaches the infintesimal dL we see that S goes to dL/r and
C differs from 1 by only a second-order term in (dL/r), so the
infintesimal rotation matrix is
_ _
| 1 0 -cos(a)(dL/r) |
m(a) = | 0 1 sin(a)(dL/r) | (3)
|_ cos(a)(dL/r) -sin(a)(dL/r) 1 _|
For a unit circle path (i.e., R=1) we have L = a, and therefore dL=da.
If we take an arc of angular size q on this path, and divide it into
n equal segments, we have da = q/n, and for the kth segment we have
a = kq/n. Making these substutions into (3) and evaluating the
product m(kq/n) for k = 1 to n in the limit as n goes to infinity,
we find that the net effect of rolling a sphere of radius r=1/sqrt(3)
all the way around a unit circle is the identity matrix. In other
words, the sphere is returned to its original orientation, in
agreement with the fact that a unit sphere rolling once around a
circle of radius R = sqrt(3) is returned to its original orientation,
as we saw previously.
We would like to have a simple expression for products of matrices
in the limit as the individual path lengths become vanishingly small
and k goes to infinity. To do this we might recall a similar
situation with respect to products of real numbers. For example,
consider how we would determine the geometric mean of the real numbers
between 0 and 1. The geometric mean G of a finite set of values v1,
v2,..,vk is simply the quantity G = (v1*v2*...*vk)^(1/k), so the
natural logarithm of G is
ln(v1) + ln(v2) + ... + ln(vk)
ln(G) = -------------------------------
k
This makes it clear that the logarithm of the geometric mean of a
continuous function v(x) from x = a to b is
b
1 /
ln(G) = ----- | ln(v(x)) dx
b - a /
x=a
For the simple case v(x) = x with x between 0 and 1 this gives
ln(G) = -1, and so the geometric mean of the real numbers from 0 to
1 is G = 1/e.
Now, by analogy, it might be tempting to suppose that the logarithm
of M(net) in (2) is just the sum of the logarithms of the matricies
M(aj), j=1,2,..,k. If this were true, we could proceed to the
continuous case, letting m(a) denote the infintessimal rotation
matrix for an incremental movement along the path, and we would
have
L1
/
ln(M(net)) = | ln[m( a(L) )] dL
/
L0
which would imply that the net re-orientation of the sphere after
rolling along the curve from L0 to L1 is given by the exponential
of this ln(M(net)). However, this assumes the logarithmic property
log(AB) = log(A)+log(B) applies to matrices, which is not generally
true, because the logarithmic property does not apply to non-commuting
entities - such as general 3D rotation matricies. To see this, notice
that exp(A)exp(B) does not generally equal exp(A+B), because this
would imply exp(A)exp(B) = exp(B)exp(A).
In view of this, it seems that some sort of non-commuting "addition"
would be needed in order to recapture the familiar logarithmic
property for arbitrary matrices. It would then be necessary to
define the analagous "ordered" integration, so the integral along
a path between any two points would depend on the direction in which
the path was traversed. Furthermore, the net effect of rolling once
around a given closed path will generally depend on the starting
point, because if we consider two points P1 and P2 on a closed loop,
and let A denote the rotation matrix given by rolling the sphere
(clockwise) along the curve from P1 to P2, and B the rotation matrix
given by rolling on from P2 around the rest of the loop to P1, then
the net re-orientation going clockwise around the loop from P1 to P1
is AB, whereas the net re-orientation going clockwise around the
loop from P2 to P2 is BA, which need not equal AB for general paths.
Nevertheless, the above formulas are applicable to rolling along
a restricted class of self-similar curves (such as straight lines),
so it's interesting to develop the formulas for rolling along an
arbitrary path based on the premise (which admittedly has only limited
validity) that the logarithmic property applies to the rotation
matrices. We could also consider the cases where rolling along a
given path length yields the same re-orientation of the sphere, and
the cases where (for closed loops) the net re-orientation around the
loop is independent of the starting point. For example, this
condition is true for perfectly circular paths on the plane.
Notice that the infintesimal rotation matrix (3) can be split into
two parts
_ _ _ _
| 1 0 0 | 1 | 0 0 -cos(a) |
m = | 0 1 0 | + --- | 0 0 sin(a) | dL (4)
|_ 0 0 1 _| r |_ cos(a) -sin(a) 0 _|
This fits nicely with the power series expansion for the logarithm
x^2 x^3
ln(1+x) = x - ----- + ----- - etc. (5)
2 3
Letting "I" denote the identity matrix, and u(a) denote the right
hand matrix in (4), we can write
/ u(a) \ u(a) u(a)^2
ln(m) = ln( I + ---- dL ) = ---- dL - ------ (dL)^2 + ... (6)
\ r / r 2r^2
so all terms after the first are second or higher order in dL/r.
Thus, in the limit as dL -> 0 we have simply ln(m) = u(a)/r dL.
As a result, if L is the path-length parameter of a plane curve that
makes an angle a(L) relative to some arbitrary axis, then (under the
assumption of the logarithmic property) the net rotation of a sphere
rolling along that curve from L0 to L1 is given by the matrix
_ _
| L1 |
| / u(a(L)) |
exp| | ------- dL | (7)
| / r |
|_ L0 _|
If a(L) is constant we recover equation (1) for finite rolling along
a straight line. Note that these rotations are indeed commutative,
so the formula is applicable. On the other hand, if we take a(L)=L
(yielding a circular path of radius R=1) and evaluate (7) for this
case (with L0 = 0 and L1 = q), we arrive at the net rotation
_ _
| -sin(q) |
| 0 0 ------- |
| r |
| |
exp| 1-cos(q) | (8)
| 0 0 -------- |
| r |
| |
| sin(q) -1+cos(q) |
| ------ --------- 0 |
|_ r r _|
Unfortunately, due to the inapplicability of the logarithmic property
for matrices, this does not correspond to the actual rotation of a
sphere rolling around a circular path, as can be seen from the fact
that it gives the identity rotation whenever q = 2pi, regardless of
the value of r, which (as we saw previously) is not correct.
The circular locus of contact points is just the points of tangency
between the sphere and the cone, and the relations between R and the
circumference of that contact circle can be inferred directly from
the diagram. Incidentally, this shows that for a "right" cone - which
means the sphere and the plane circle have the same radius - the ratio
of contact circumferences is q = sqrt(1+1^2) = sqrt(2), so the sphere
will never return precisely to its initial configuration.
Now consider an arbitrary curve drawn on a flat surface, and a sphere
rolling (without slipping or spinning) along this curve. We can
parameterize the curve by giving the tangent angle "a" (relative to
an arbitrarily chosen axis) as a function of the distance along the
curve. If the sphere rolls along a straight line with angle "a" for
a finite distance L, the change in the orientation of the sphere is
given by multiplying the initial orientation by the rotation matrix
_ _
| ccC+ss cs(1-C) -cS |
M = | cs(1-C) ssC+cc sS | (1)
|_ cS -sS C _|
where c=cos(a), s=sin(a), C=cos(L/r), and S=sin(L/r) and r is the
radius of the sphere.
The net change in orientation after the sphere has rolled along k
linear segments, each of length L with the path angles a1, a2,...ak,
is given by the matrix product
M(net) = M(a1) M(a2) .... M(ak) (2)
As L approaches the infintesimal dL we see that S goes to dL/r and
C differs from 1 by only a second-order term in (dL/r), so the
infintesimal rotation matrix is
_ _
| 1 0 -cos(a)(dL/r) |
m(a) = | 0 1 sin(a)(dL/r) | (3)
|_ cos(a)(dL/r) -sin(a)(dL/r) 1 _|
For a unit circle path (i.e., R=1) we have L = a, and therefore dL=da.
If we take an arc of angular size q on this path, and divide it into
n equal segments, we have da = q/n, and for the kth segment we have
a = kq/n. Making these substutions into (3) and evaluating the
product m(kq/n) for k = 1 to n in the limit as n goes to infinity,
we find that the net effect of rolling a sphere of radius r=1/sqrt(3)
all the way around a unit circle is the identity matrix. In other
words, the sphere is returned to its original orientation, in
agreement with the fact that a unit sphere rolling once around a
circle of radius R = sqrt(3) is returned to its original orientation,
as we saw previously.
We would like to have a simple expression for products of matrices
in the limit as the individual path lengths become vanishingly small
and k goes to infinity. To do this we might recall a similar
situation with respect to products of real numbers. For example,
consider how we would determine the geometric mean of the real numbers
between 0 and 1. The geometric mean G of a finite set of values v1,
v2,..,vk is simply the quantity G = (v1*v2*...*vk)^(1/k), so the
natural logarithm of G is
ln(v1) + ln(v2) + ... + ln(vk)
ln(G) = -------------------------------
k
This makes it clear that the logarithm of the geometric mean of a
continuous function v(x) from x = a to b is
b
1 /
ln(G) = ----- | ln(v(x)) dx
b - a /
x=a
For the simple case v(x) = x with x between 0 and 1 this gives
ln(G) = -1, and so the geometric mean of the real numbers from 0 to
1 is G = 1/e.
Now, by analogy, it might be tempting to suppose that the logarithm
of M(net) in (2) is just the sum of the logarithms of the matricies
M(aj), j=1,2,..,k. If this were true, we could proceed to the
continuous case, letting m(a) denote the infintessimal rotation
matrix for an incremental movement along the path, and we would
have
L1
/
ln(M(net)) = | ln[m( a(L) )] dL
/
L0
which would imply that the net re-orientation of the sphere after
rolling along the curve from L0 to L1 is given by the exponential
of this ln(M(net)). However, this assumes the logarithmic property
log(AB) = log(A)+log(B) applies to matrices, which is not generally
true, because the logarithmic property does not apply to non-commuting
entities - such as general 3D rotation matricies. To see this, notice
that exp(A)exp(B) does not generally equal exp(A+B), because this
would imply exp(A)exp(B) = exp(B)exp(A).
In view of this, it seems that some sort of non-commuting "addition"
would be needed in order to recapture the familiar logarithmic
property for arbitrary matrices. It would then be necessary to
define the analagous "ordered" integration, so the integral along
a path between any two points would depend on the direction in which
the path was traversed. Furthermore, the net effect of rolling once
around a given closed path will generally depend on the starting
point, because if we consider two points P1 and P2 on a closed loop,
and let A denote the rotation matrix given by rolling the sphere
(clockwise) along the curve from P1 to P2, and B the rotation matrix
given by rolling on from P2 around the rest of the loop to P1, then
the net re-orientation going clockwise around the loop from P1 to P1
is AB, whereas the net re-orientation going clockwise around the
loop from P2 to P2 is BA, which need not equal AB for general paths.
Nevertheless, the above formulas are applicable to rolling along
a restricted class of self-similar curves (such as straight lines),
so it's interesting to develop the formulas for rolling along an
arbitrary path based on the premise (which admittedly has only limited
validity) that the logarithmic property applies to the rotation
matrices. We could also consider the cases where rolling along a
given path length yields the same re-orientation of the sphere, and
the cases where (for closed loops) the net re-orientation around the
loop is independent of the starting point. For example, this
condition is true for perfectly circular paths on the plane.
Notice that the infintesimal rotation matrix (3) can be split into
two parts
_ _ _ _
| 1 0 0 | 1 | 0 0 -cos(a) |
m = | 0 1 0 | + --- | 0 0 sin(a) | dL (4)
|_ 0 0 1 _| r |_ cos(a) -sin(a) 0 _|
This fits nicely with the power series expansion for the logarithm
x^2 x^3
ln(1+x) = x - ----- + ----- - etc. (5)
2 3
Letting "I" denote the identity matrix, and u(a) denote the right
hand matrix in (4), we can write
/ u(a) \ u(a) u(a)^2
ln(m) = ln( I + ---- dL ) = ---- dL - ------ (dL)^2 + ... (6)
\ r / r 2r^2
so all terms after the first are second or higher order in dL/r.
Thus, in the limit as dL -> 0 we have simply ln(m) = u(a)/r dL.
As a result, if L is the path-length parameter of a plane curve that
makes an angle a(L) relative to some arbitrary axis, then (under the
assumption of the logarithmic property) the net rotation of a sphere
rolling along that curve from L0 to L1 is given by the matrix
_ _
| L1 |
| / u(a(L)) |
exp| | ------- dL | (7)
| / r |
|_ L0 _|
If a(L) is constant we recover equation (1) for finite rolling along
a straight line. Note that these rotations are indeed commutative,
so the formula is applicable. On the other hand, if we take a(L)=L
(yielding a circular path of radius R=1) and evaluate (7) for this
case (with L0 = 0 and L1 = q), we arrive at the net rotation
_ _
| -sin(q) |
| 0 0 ------- |
| r |
| |
exp| 1-cos(q) | (8)
| 0 0 -------- |
| r |
| |
| sin(q) -1+cos(q) |
| ------ --------- 0 |
|_ r r _|
Unfortunately, due to the inapplicability of the logarithmic property
for matrices, this does not correspond to the actual rotation of a
sphere rolling around a circular path, as can be seen from the fact
that it gives the identity rotation whenever q = 2pi, regardless of
the value of r, which (as we saw previously) is not correct.
Return to MathPages Main Menu
Сайт управляется системой
uCoz The circular locus of contact points is just the points of tangency
between the sphere and the cone, and the relations between R and the
circumference of that contact circle can be inferred directly from
the diagram. Incidentally, this shows that for a "right" cone - which
means the sphere and the plane circle have the same radius - the ratio
of contact circumferences is q = sqrt(1+1^2) = sqrt(2), so the sphere
will never return precisely to its initial configuration.
Now consider an arbitrary curve drawn on a flat surface, and a sphere
rolling (without slipping or spinning) along this curve. We can
parameterize the curve by giving the tangent angle "a" (relative to
an arbitrarily chosen axis) as a function of the distance along the
curve. If the sphere rolls along a straight line with angle "a" for
a finite distance L, the change in the orientation of the sphere is
given by multiplying the initial orientation by the rotation matrix
_ _
| ccC+ss cs(1-C) -cS |
M = | cs(1-C) ssC+cc sS | (1)
|_ cS -sS C _|
where c=cos(a), s=sin(a), C=cos(L/r), and S=sin(L/r) and r is the
radius of the sphere.
The net change in orientation after the sphere has rolled along k
linear segments, each of length L with the path angles a1, a2,...ak,
is given by the matrix product
M(net) = M(a1) M(a2) .... M(ak) (2)
As L approaches the infintesimal dL we see that S goes to dL/r and
C differs from 1 by only a second-order term in (dL/r), so the
infintesimal rotation matrix is
_ _
| 1 0 -cos(a)(dL/r) |
m(a) = | 0 1 sin(a)(dL/r) | (3)
|_ cos(a)(dL/r) -sin(a)(dL/r) 1 _|
For a unit circle path (i.e., R=1) we have L = a, and therefore dL=da.
If we take an arc of angular size q on this path, and divide it into
n equal segments, we have da = q/n, and for the kth segment we have
a = kq/n. Making these substutions into (3) and evaluating the
product m(kq/n) for k = 1 to n in the limit as n goes to infinity,
we find that the net effect of rolling a sphere of radius r=1/sqrt(3)
all the way around a unit circle is the identity matrix. In other
words, the sphere is returned to its original orientation, in
agreement with the fact that a unit sphere rolling once around a
circle of radius R = sqrt(3) is returned to its original orientation,
as we saw previously.
We would like to have a simple expression for products of matrices
in the limit as the individual path lengths become vanishingly small
and k goes to infinity. To do this we might recall a similar
situation with respect to products of real numbers. For example,
consider how we would determine the geometric mean of the real numbers
between 0 and 1. The geometric mean G of a finite set of values v1,
v2,..,vk is simply the quantity G = (v1*v2*...*vk)^(1/k), so the
natural logarithm of G is
ln(v1) + ln(v2) + ... + ln(vk)
ln(G) = -------------------------------
k
This makes it clear that the logarithm of the geometric mean of a
continuous function v(x) from x = a to b is
b
1 /
ln(G) = ----- | ln(v(x)) dx
b - a /
x=a
For the simple case v(x) = x with x between 0 and 1 this gives
ln(G) = -1, and so the geometric mean of the real numbers from 0 to
1 is G = 1/e.
Now, by analogy, it might be tempting to suppose that the logarithm
of M(net) in (2) is just the sum of the logarithms of the matricies
M(aj), j=1,2,..,k. If this were true, we could proceed to the
continuous case, letting m(a) denote the infintessimal rotation
matrix for an incremental movement along the path, and we would
have
L1
/
ln(M(net)) = | ln[m( a(L) )] dL
/
L0
which would imply that the net re-orientation of the sphere after
rolling along the curve from L0 to L1 is given by the exponential
of this ln(M(net)). However, this assumes the logarithmic property
log(AB) = log(A)+log(B) applies to matrices, which is not generally
true, because the logarithmic property does not apply to non-commuting
entities - such as general 3D rotation matricies. To see this, notice
that exp(A)exp(B) does not generally equal exp(A+B), because this
would imply exp(A)exp(B) = exp(B)exp(A).
In view of this, it seems that some sort of non-commuting "addition"
would be needed in order to recapture the familiar logarithmic
property for arbitrary matrices. It would then be necessary to
define the analagous "ordered" integration, so the integral along
a path between any two points would depend on the direction in which
the path was traversed. Furthermore, the net effect of rolling once
around a given closed path will generally depend on the starting
point, because if we consider two points P1 and P2 on a closed loop,
and let A denote the rotation matrix given by rolling the sphere
(clockwise) along the curve from P1 to P2, and B the rotation matrix
given by rolling on from P2 around the rest of the loop to P1, then
the net re-orientation going clockwise around the loop from P1 to P1
is AB, whereas the net re-orientation going clockwise around the
loop from P2 to P2 is BA, which need not equal AB for general paths.
Nevertheless, the above formulas are applicable to rolling along
a restricted class of self-similar curves (such as straight lines),
so it's interesting to develop the formulas for rolling along an
arbitrary path based on the premise (which admittedly has only limited
validity) that the logarithmic property applies to the rotation
matrices. We could also consider the cases where rolling along a
given path length yields the same re-orientation of the sphere, and
the cases where (for closed loops) the net re-orientation around the
loop is independent of the starting point. For example, this
condition is true for perfectly circular paths on the plane.
Notice that the infintesimal rotation matrix (3) can be split into
two parts
_ _ _ _
| 1 0 0 | 1 | 0 0 -cos(a) |
m = | 0 1 0 | + --- | 0 0 sin(a) | dL (4)
|_ 0 0 1 _| r |_ cos(a) -sin(a) 0 _|
This fits nicely with the power series expansion for the logarithm
x^2 x^3
ln(1+x) = x - ----- + ----- - etc. (5)
2 3
Letting "I" denote the identity matrix, and u(a) denote the right
hand matrix in (4), we can write
/ u(a) \ u(a) u(a)^2
ln(m) = ln( I + ---- dL ) = ---- dL - ------ (dL)^2 + ... (6)
\ r / r 2r^2
so all terms after the first are second or higher order in dL/r.
Thus, in the limit as dL -> 0 we have simply ln(m) = u(a)/r dL.
As a result, if L is the path-length parameter of a plane curve that
makes an angle a(L) relative to some arbitrary axis, then (under the
assumption of the logarithmic property) the net rotation of a sphere
rolling along that curve from L0 to L1 is given by the matrix
_ _
| L1 |
| / u(a(L)) |
exp| | ------- dL | (7)
| / r |
|_ L0 _|
If a(L) is constant we recover equation (1) for finite rolling along
a straight line. Note that these rotations are indeed commutative,
so the formula is applicable. On the other hand, if we take a(L)=L
(yielding a circular path of radius R=1) and evaluate (7) for this
case (with L0 = 0 and L1 = q), we arrive at the net rotation
_ _
| -sin(q) |
| 0 0 ------- |
| r |
| |
exp| 1-cos(q) | (8)
| 0 0 -------- |
| r |
| |
| sin(q) -1+cos(q) |
| ------ --------- 0 |
|_ r r _|
Unfortunately, due to the inapplicability of the logarithmic property
for matrices, this does not correspond to the actual rotation of a
sphere rolling around a circular path, as can be seen from the fact
that it gives the identity rotation whenever q = 2pi, regardless of
the value of r, which (as we saw previously) is not correct.
The circular locus of contact points is just the points of tangency
between the sphere and the cone, and the relations between R and the
circumference of that contact circle can be inferred directly from
the diagram. Incidentally, this shows that for a "right" cone - which
means the sphere and the plane circle have the same radius - the ratio
of contact circumferences is q = sqrt(1+1^2) = sqrt(2), so the sphere
will never return precisely to its initial configuration.
Now consider an arbitrary curve drawn on a flat surface, and a sphere
rolling (without slipping or spinning) along this curve. We can
parameterize the curve by giving the tangent angle "a" (relative to
an arbitrarily chosen axis) as a function of the distance along the
curve. If the sphere rolls along a straight line with angle "a" for
a finite distance L, the change in the orientation of the sphere is
given by multiplying the initial orientation by the rotation matrix
_ _
| ccC+ss cs(1-C) -cS |
M = | cs(1-C) ssC+cc sS | (1)
|_ cS -sS C _|
where c=cos(a), s=sin(a), C=cos(L/r), and S=sin(L/r) and r is the
radius of the sphere.
The net change in orientation after the sphere has rolled along k
linear segments, each of length L with the path angles a1, a2,...ak,
is given by the matrix product
M(net) = M(a1) M(a2) .... M(ak) (2)
As L approaches the infintesimal dL we see that S goes to dL/r and
C differs from 1 by only a second-order term in (dL/r), so the
infintesimal rotation matrix is
_ _
| 1 0 -cos(a)(dL/r) |
m(a) = | 0 1 sin(a)(dL/r) | (3)
|_ cos(a)(dL/r) -sin(a)(dL/r) 1 _|
For a unit circle path (i.e., R=1) we have L = a, and therefore dL=da.
If we take an arc of angular size q on this path, and divide it into
n equal segments, we have da = q/n, and for the kth segment we have
a = kq/n. Making these substutions into (3) and evaluating the
product m(kq/n) for k = 1 to n in the limit as n goes to infinity,
we find that the net effect of rolling a sphere of radius r=1/sqrt(3)
all the way around a unit circle is the identity matrix. In other
words, the sphere is returned to its original orientation, in
agreement with the fact that a unit sphere rolling once around a
circle of radius R = sqrt(3) is returned to its original orientation,
as we saw previously.
We would like to have a simple expression for products of matrices
in the limit as the individual path lengths become vanishingly small
and k goes to infinity. To do this we might recall a similar
situation with respect to products of real numbers. For example,
consider how we would determine the geometric mean of the real numbers
between 0 and 1. The geometric mean G of a finite set of values v1,
v2,..,vk is simply the quantity G = (v1*v2*...*vk)^(1/k), so the
natural logarithm of G is
ln(v1) + ln(v2) + ... + ln(vk)
ln(G) = -------------------------------
k
This makes it clear that the logarithm of the geometric mean of a
continuous function v(x) from x = a to b is
b
1 /
ln(G) = ----- | ln(v(x)) dx
b - a /
x=a
For the simple case v(x) = x with x between 0 and 1 this gives
ln(G) = -1, and so the geometric mean of the real numbers from 0 to
1 is G = 1/e.
Now, by analogy, it might be tempting to suppose that the logarithm
of M(net) in (2) is just the sum of the logarithms of the matricies
M(aj), j=1,2,..,k. If this were true, we could proceed to the
continuous case, letting m(a) denote the infintessimal rotation
matrix for an incremental movement along the path, and we would
have
L1
/
ln(M(net)) = | ln[m( a(L) )] dL
/
L0
which would imply that the net re-orientation of the sphere after
rolling along the curve from L0 to L1 is given by the exponential
of this ln(M(net)). However, this assumes the logarithmic property
log(AB) = log(A)+log(B) applies to matrices, which is not generally
true, because the logarithmic property does not apply to non-commuting
entities - such as general 3D rotation matricies. To see this, notice
that exp(A)exp(B) does not generally equal exp(A+B), because this
would imply exp(A)exp(B) = exp(B)exp(A).
In view of this, it seems that some sort of non-commuting "addition"
would be needed in order to recapture the familiar logarithmic
property for arbitrary matrices. It would then be necessary to
define the analagous "ordered" integration, so the integral along
a path between any two points would depend on the direction in which
the path was traversed. Furthermore, the net effect of rolling once
around a given closed path will generally depend on the starting
point, because if we consider two points P1 and P2 on a closed loop,
and let A denote the rotation matrix given by rolling the sphere
(clockwise) along the curve from P1 to P2, and B the rotation matrix
given by rolling on from P2 around the rest of the loop to P1, then
the net re-orientation going clockwise around the loop from P1 to P1
is AB, whereas the net re-orientation going clockwise around the
loop from P2 to P2 is BA, which need not equal AB for general paths.
Nevertheless, the above formulas are applicable to rolling along
a restricted class of self-similar curves (such as straight lines),
so it's interesting to develop the formulas for rolling along an
arbitrary path based on the premise (which admittedly has only limited
validity) that the logarithmic property applies to the rotation
matrices. We could also consider the cases where rolling along a
given path length yields the same re-orientation of the sphere, and
the cases where (for closed loops) the net re-orientation around the
loop is independent of the starting point. For example, this
condition is true for perfectly circular paths on the plane.
Notice that the infintesimal rotation matrix (3) can be split into
two parts
_ _ _ _
| 1 0 0 | 1 | 0 0 -cos(a) |
m = | 0 1 0 | + --- | 0 0 sin(a) | dL (4)
|_ 0 0 1 _| r |_ cos(a) -sin(a) 0 _|
This fits nicely with the power series expansion for the logarithm
x^2 x^3
ln(1+x) = x - ----- + ----- - etc. (5)
2 3
Letting "I" denote the identity matrix, and u(a) denote the right
hand matrix in (4), we can write
/ u(a) \ u(a) u(a)^2
ln(m) = ln( I + ---- dL ) = ---- dL - ------ (dL)^2 + ... (6)
\ r / r 2r^2
so all terms after the first are second or higher order in dL/r.
Thus, in the limit as dL -> 0 we have simply ln(m) = u(a)/r dL.
As a result, if L is the path-length parameter of a plane curve that
makes an angle a(L) relative to some arbitrary axis, then (under the
assumption of the logarithmic property) the net rotation of a sphere
rolling along that curve from L0 to L1 is given by the matrix
_ _
| L1 |
| / u(a(L)) |
exp| | ------- dL | (7)
| / r |
|_ L0 _|
If a(L) is constant we recover equation (1) for finite rolling along
a straight line. Note that these rotations are indeed commutative,
so the formula is applicable. On the other hand, if we take a(L)=L
(yielding a circular path of radius R=1) and evaluate (7) for this
case (with L0 = 0 and L1 = q), we arrive at the net rotation
_ _
| -sin(q) |
| 0 0 ------- |
| r |
| |
exp| 1-cos(q) | (8)
| 0 0 -------- |
| r |
| |
| sin(q) -1+cos(q) |
| ------ --------- 0 |
|_ r r _|
Unfortunately, due to the inapplicability of the logarithmic property
for matrices, this does not correspond to the actual rotation of a
sphere rolling around a circular path, as can be seen from the fact
that it gives the identity rotation whenever q = 2pi, regardless of
the value of r, which (as we saw previously) is not correct.