Net Area and Green's Theorem
Given the coordinates of the vertices of a triangle in the plane
(with respect to an orthogonal xy coordinate system), what is the
enclosed area of the triangle? Consider an arbitrary triangle
such as the one shown below
 Figure 1
We are given the coordinates of the verticies (x1,y1), (x2,y2), and
(x3,y3), and we wish to determine the enclosed area? It's helpful to
inscribe the triangle inside a square as shown below
Figure 1
We are given the coordinates of the verticies (x1,y1), (x2,y2), and
(x3,y3), and we wish to determine the enclosed area? It's helpful to
inscribe the triangle inside a square as shown below
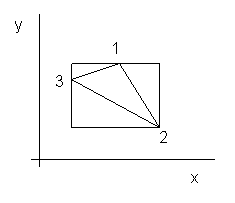 Figure 2
Clearly the area inside the triangle is just the area of the enclosing
rectangle minus the areas of the three surrounding right triangles.
Thus we have
A = (x2-x3)(y1-y2)
(y3-y2)(x2-x3) (y1-y3)(x1-x3) (y1-y2)(x2-x1)
- -------------- - -------------- - --------------
2 2 2
which answers our original question. Now, we could expand the products
in the above expression and try to simplify it, but its easier to
observe that the three exterior right triangles are each half of a
rectangle (cut diagonally), and that those three rectangles fill up
the overall rectangle, with two of them overlapping in one rectangular
corner. Therefore, the area of the three exterior triangles is simply
half of the difference between the overall rectangle and the overlapped
rectangle. Subtracting this from the area of the overall rectangle
immediately gives the area of the original triangle
(x2-x3)(y1-y2) - (x1-x2)(y2-y3)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x1y3-x3y1) )
2 \ /
In this same way it's easy to deduce that the area enclosed by a
general quadralateral can be expressed in terms of the coordinates
of its verticies as
(x2-x4)(y1-y3) - (x1-x3)(y2-y4)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x4y3-x3y4) + (x1y4-x4y1) )
2 \ /
It's worth noting that, assuming all the verticies are in the ++
quadrant of the xy coordinate system (i.e., all the coordinates are
positive), these formulas give the positive area only if the verticies
are numbered clockwise around the perimeter. If they are counter-
clockwise, the computed area is negative. Of course, a quadralateral
can have crossing edges, such that the verticies are clockwise around
one region and counter-clockwise around the other. Thus, the computed
area of a non-degenerate quadralateral can vanish, as in the case of
the quadralateral shown in Figure 3.
Figure 2
Clearly the area inside the triangle is just the area of the enclosing
rectangle minus the areas of the three surrounding right triangles.
Thus we have
A = (x2-x3)(y1-y2)
(y3-y2)(x2-x3) (y1-y3)(x1-x3) (y1-y2)(x2-x1)
- -------------- - -------------- - --------------
2 2 2
which answers our original question. Now, we could expand the products
in the above expression and try to simplify it, but its easier to
observe that the three exterior right triangles are each half of a
rectangle (cut diagonally), and that those three rectangles fill up
the overall rectangle, with two of them overlapping in one rectangular
corner. Therefore, the area of the three exterior triangles is simply
half of the difference between the overall rectangle and the overlapped
rectangle. Subtracting this from the area of the overall rectangle
immediately gives the area of the original triangle
(x2-x3)(y1-y2) - (x1-x2)(y2-y3)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x1y3-x3y1) )
2 \ /
In this same way it's easy to deduce that the area enclosed by a
general quadralateral can be expressed in terms of the coordinates
of its verticies as
(x2-x4)(y1-y3) - (x1-x3)(y2-y4)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x4y3-x3y4) + (x1y4-x4y1) )
2 \ /
It's worth noting that, assuming all the verticies are in the ++
quadrant of the xy coordinate system (i.e., all the coordinates are
positive), these formulas give the positive area only if the verticies
are numbered clockwise around the perimeter. If they are counter-
clockwise, the computed area is negative. Of course, a quadralateral
can have crossing edges, such that the verticies are clockwise around
one region and counter-clockwise around the other. Thus, the computed
area of a non-degenerate quadralateral can vanish, as in the case of
the quadralateral shown in Figure 3.
 Figure 3
It's interesting to consider the correspondence between the "net area"
(as defined by the above formula) associated with four points in the
plane and the squared intervals in geometries with non-positive-
definite metrics.
Anyway, continuing with this same approach, we find that the "net
area" enclosed by a general n-sided polygon is given by
1 n / \
A = - SUM ( x[i+1] y[i] - x[i] y[i+1] )
2 i=1 \ /
with the understanding that x[n+1] = x[1] and y[n+1] = y[1]. Taking
this to the limit as n goes to infinity, we have the signed net area
enclosed by any closed loop in the plane
1 / / \
A = - | ( (x+dx)y - x(y+dy) )
2 / \ /
1 /
= - | (ydx - xdy)
2 /
where the integral is evaluated once around the loop. Therefore, if
we have a parametric closed curve in the plane where x=x(s) and y=y(s)
then we can write the area net formula as
1 / / dx dy \
A = - | ( y -- - x -- ) ds
2 / \ ds ds /
For example, consider an ellipse with major radius R and minor radius
r. Centered at the origin and oriented appropriately, the boundary
of this ellipse is given by the parametric equations
x = R cos(a) y = r sin(a)
where the paramater "a" is the angle that varies from 0 to 2pi as
we proceed around the loop (counter clockwise, so our area will be
negative). The derivatives of x and y are
dx dy
-- = -R sin(a) -- = r cos(a)
da da
so the enclosed area is
2pi
1 / / \
A = - | -Rr ( sin(a)^2 + cos(a)^2 ) ds
2 / \ /
s=0
Since the quantity inside the parantheses is identically 1, we have
2pi
1 / Rr |2pi
A = - - | Rr da = - --- a | = - pi Rr
2 / 2 |0
a=0
as expected. This example illustrates that, because of the symmetry
between x and y, the above area formula sometimes leads to very
simple (even trivial) integrals when evaluating the areas enclosed
within parametrically defined curves.
The above is is essentially just an application of Green's Theorem,
which states that if we have two differentiable scalar fields P(x,y)
and Q(x,y) over a (regular) region R of the xy plane enclosed by the
curve C, then we have the following equality between a double integral
over the region and a line integral around the boundary curve
/ / / DQ DP \ /
| | ( -- - -- ) dx dy = | (Qdy + Pdx)
/ / \ Dx Dy / /
R C
where "D" denotes partial derivatives. To show how this reduces to
the simple area formula, notice that if we set Q=x and P=-y then
DQ/Dx = 1 and DP/Dy = -1, and Green's Theorem reduces to
/ / /
| | 2 dx dy = | (xdy - ydx)
/ / /
R C
The left side is twice the area of the enclosed region R, and the
right side is twice our previous formula for the area (with the
opposite sign convention).
Figure 3
It's interesting to consider the correspondence between the "net area"
(as defined by the above formula) associated with four points in the
plane and the squared intervals in geometries with non-positive-
definite metrics.
Anyway, continuing with this same approach, we find that the "net
area" enclosed by a general n-sided polygon is given by
1 n / \
A = - SUM ( x[i+1] y[i] - x[i] y[i+1] )
2 i=1 \ /
with the understanding that x[n+1] = x[1] and y[n+1] = y[1]. Taking
this to the limit as n goes to infinity, we have the signed net area
enclosed by any closed loop in the plane
1 / / \
A = - | ( (x+dx)y - x(y+dy) )
2 / \ /
1 /
= - | (ydx - xdy)
2 /
where the integral is evaluated once around the loop. Therefore, if
we have a parametric closed curve in the plane where x=x(s) and y=y(s)
then we can write the area net formula as
1 / / dx dy \
A = - | ( y -- - x -- ) ds
2 / \ ds ds /
For example, consider an ellipse with major radius R and minor radius
r. Centered at the origin and oriented appropriately, the boundary
of this ellipse is given by the parametric equations
x = R cos(a) y = r sin(a)
where the paramater "a" is the angle that varies from 0 to 2pi as
we proceed around the loop (counter clockwise, so our area will be
negative). The derivatives of x and y are
dx dy
-- = -R sin(a) -- = r cos(a)
da da
so the enclosed area is
2pi
1 / / \
A = - | -Rr ( sin(a)^2 + cos(a)^2 ) ds
2 / \ /
s=0
Since the quantity inside the parantheses is identically 1, we have
2pi
1 / Rr |2pi
A = - - | Rr da = - --- a | = - pi Rr
2 / 2 |0
a=0
as expected. This example illustrates that, because of the symmetry
between x and y, the above area formula sometimes leads to very
simple (even trivial) integrals when evaluating the areas enclosed
within parametrically defined curves.
The above is is essentially just an application of Green's Theorem,
which states that if we have two differentiable scalar fields P(x,y)
and Q(x,y) over a (regular) region R of the xy plane enclosed by the
curve C, then we have the following equality between a double integral
over the region and a line integral around the boundary curve
/ / / DQ DP \ /
| | ( -- - -- ) dx dy = | (Qdy + Pdx)
/ / \ Dx Dy / /
R C
where "D" denotes partial derivatives. To show how this reduces to
the simple area formula, notice that if we set Q=x and P=-y then
DQ/Dx = 1 and DP/Dy = -1, and Green's Theorem reduces to
/ / /
| | 2 dx dy = | (xdy - ydx)
/ / /
R C
The left side is twice the area of the enclosed region R, and the
right side is twice our previous formula for the area (with the
opposite sign convention).
Return to MathPages Main Menu
Сайт управляется системой
uCoz Figure 1
We are given the coordinates of the verticies (x1,y1), (x2,y2), and
(x3,y3), and we wish to determine the enclosed area? It's helpful to
inscribe the triangle inside a square as shown below
Figure 1
We are given the coordinates of the verticies (x1,y1), (x2,y2), and
(x3,y3), and we wish to determine the enclosed area? It's helpful to
inscribe the triangle inside a square as shown below
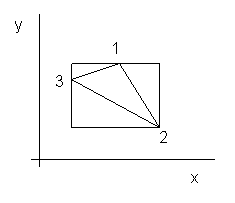 Figure 2
Clearly the area inside the triangle is just the area of the enclosing
rectangle minus the areas of the three surrounding right triangles.
Thus we have
A = (x2-x3)(y1-y2)
(y3-y2)(x2-x3) (y1-y3)(x1-x3) (y1-y2)(x2-x1)
- -------------- - -------------- - --------------
2 2 2
which answers our original question. Now, we could expand the products
in the above expression and try to simplify it, but its easier to
observe that the three exterior right triangles are each half of a
rectangle (cut diagonally), and that those three rectangles fill up
the overall rectangle, with two of them overlapping in one rectangular
corner. Therefore, the area of the three exterior triangles is simply
half of the difference between the overall rectangle and the overlapped
rectangle. Subtracting this from the area of the overall rectangle
immediately gives the area of the original triangle
(x2-x3)(y1-y2) - (x1-x2)(y2-y3)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x1y3-x3y1) )
2 \ /
In this same way it's easy to deduce that the area enclosed by a
general quadralateral can be expressed in terms of the coordinates
of its verticies as
(x2-x4)(y1-y3) - (x1-x3)(y2-y4)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x4y3-x3y4) + (x1y4-x4y1) )
2 \ /
It's worth noting that, assuming all the verticies are in the ++
quadrant of the xy coordinate system (i.e., all the coordinates are
positive), these formulas give the positive area only if the verticies
are numbered clockwise around the perimeter. If they are counter-
clockwise, the computed area is negative. Of course, a quadralateral
can have crossing edges, such that the verticies are clockwise around
one region and counter-clockwise around the other. Thus, the computed
area of a non-degenerate quadralateral can vanish, as in the case of
the quadralateral shown in Figure 3.
Figure 2
Clearly the area inside the triangle is just the area of the enclosing
rectangle minus the areas of the three surrounding right triangles.
Thus we have
A = (x2-x3)(y1-y2)
(y3-y2)(x2-x3) (y1-y3)(x1-x3) (y1-y2)(x2-x1)
- -------------- - -------------- - --------------
2 2 2
which answers our original question. Now, we could expand the products
in the above expression and try to simplify it, but its easier to
observe that the three exterior right triangles are each half of a
rectangle (cut diagonally), and that those three rectangles fill up
the overall rectangle, with two of them overlapping in one rectangular
corner. Therefore, the area of the three exterior triangles is simply
half of the difference between the overall rectangle and the overlapped
rectangle. Subtracting this from the area of the overall rectangle
immediately gives the area of the original triangle
(x2-x3)(y1-y2) - (x1-x2)(y2-y3)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x1y3-x3y1) )
2 \ /
In this same way it's easy to deduce that the area enclosed by a
general quadralateral can be expressed in terms of the coordinates
of its verticies as
(x2-x4)(y1-y3) - (x1-x3)(y2-y4)
A = -------------------------------
2
1 / \
= - ( (x2y1-x1y2) + (x3y2-x2y3) + (x4y3-x3y4) + (x1y4-x4y1) )
2 \ /
It's worth noting that, assuming all the verticies are in the ++
quadrant of the xy coordinate system (i.e., all the coordinates are
positive), these formulas give the positive area only if the verticies
are numbered clockwise around the perimeter. If they are counter-
clockwise, the computed area is negative. Of course, a quadralateral
can have crossing edges, such that the verticies are clockwise around
one region and counter-clockwise around the other. Thus, the computed
area of a non-degenerate quadralateral can vanish, as in the case of
the quadralateral shown in Figure 3.
 Figure 3
It's interesting to consider the correspondence between the "net area"
(as defined by the above formula) associated with four points in the
plane and the squared intervals in geometries with non-positive-
definite metrics.
Anyway, continuing with this same approach, we find that the "net
area" enclosed by a general n-sided polygon is given by
1 n / \
A = - SUM ( x[i+1] y[i] - x[i] y[i+1] )
2 i=1 \ /
with the understanding that x[n+1] = x[1] and y[n+1] = y[1]. Taking
this to the limit as n goes to infinity, we have the signed net area
enclosed by any closed loop in the plane
1 / / \
A = - | ( (x+dx)y - x(y+dy) )
2 / \ /
1 /
= - | (ydx - xdy)
2 /
where the integral is evaluated once around the loop. Therefore, if
we have a parametric closed curve in the plane where x=x(s) and y=y(s)
then we can write the area net formula as
1 / / dx dy \
A = - | ( y -- - x -- ) ds
2 / \ ds ds /
For example, consider an ellipse with major radius R and minor radius
r. Centered at the origin and oriented appropriately, the boundary
of this ellipse is given by the parametric equations
x = R cos(a) y = r sin(a)
where the paramater "a" is the angle that varies from 0 to 2pi as
we proceed around the loop (counter clockwise, so our area will be
negative). The derivatives of x and y are
dx dy
-- = -R sin(a) -- = r cos(a)
da da
so the enclosed area is
2pi
1 / / \
A = - | -Rr ( sin(a)^2 + cos(a)^2 ) ds
2 / \ /
s=0
Since the quantity inside the parantheses is identically 1, we have
2pi
1 / Rr |2pi
A = - - | Rr da = - --- a | = - pi Rr
2 / 2 |0
a=0
as expected. This example illustrates that, because of the symmetry
between x and y, the above area formula sometimes leads to very
simple (even trivial) integrals when evaluating the areas enclosed
within parametrically defined curves.
The above is is essentially just an application of Green's Theorem,
which states that if we have two differentiable scalar fields P(x,y)
and Q(x,y) over a (regular) region R of the xy plane enclosed by the
curve C, then we have the following equality between a double integral
over the region and a line integral around the boundary curve
/ / / DQ DP \ /
| | ( -- - -- ) dx dy = | (Qdy + Pdx)
/ / \ Dx Dy / /
R C
where "D" denotes partial derivatives. To show how this reduces to
the simple area formula, notice that if we set Q=x and P=-y then
DQ/Dx = 1 and DP/Dy = -1, and Green's Theorem reduces to
/ / /
| | 2 dx dy = | (xdy - ydx)
/ / /
R C
The left side is twice the area of the enclosed region R, and the
right side is twice our previous formula for the area (with the
opposite sign convention).
Figure 3
It's interesting to consider the correspondence between the "net area"
(as defined by the above formula) associated with four points in the
plane and the squared intervals in geometries with non-positive-
definite metrics.
Anyway, continuing with this same approach, we find that the "net
area" enclosed by a general n-sided polygon is given by
1 n / \
A = - SUM ( x[i+1] y[i] - x[i] y[i+1] )
2 i=1 \ /
with the understanding that x[n+1] = x[1] and y[n+1] = y[1]. Taking
this to the limit as n goes to infinity, we have the signed net area
enclosed by any closed loop in the plane
1 / / \
A = - | ( (x+dx)y - x(y+dy) )
2 / \ /
1 /
= - | (ydx - xdy)
2 /
where the integral is evaluated once around the loop. Therefore, if
we have a parametric closed curve in the plane where x=x(s) and y=y(s)
then we can write the area net formula as
1 / / dx dy \
A = - | ( y -- - x -- ) ds
2 / \ ds ds /
For example, consider an ellipse with major radius R and minor radius
r. Centered at the origin and oriented appropriately, the boundary
of this ellipse is given by the parametric equations
x = R cos(a) y = r sin(a)
where the paramater "a" is the angle that varies from 0 to 2pi as
we proceed around the loop (counter clockwise, so our area will be
negative). The derivatives of x and y are
dx dy
-- = -R sin(a) -- = r cos(a)
da da
so the enclosed area is
2pi
1 / / \
A = - | -Rr ( sin(a)^2 + cos(a)^2 ) ds
2 / \ /
s=0
Since the quantity inside the parantheses is identically 1, we have
2pi
1 / Rr |2pi
A = - - | Rr da = - --- a | = - pi Rr
2 / 2 |0
a=0
as expected. This example illustrates that, because of the symmetry
between x and y, the above area formula sometimes leads to very
simple (even trivial) integrals when evaluating the areas enclosed
within parametrically defined curves.
The above is is essentially just an application of Green's Theorem,
which states that if we have two differentiable scalar fields P(x,y)
and Q(x,y) over a (regular) region R of the xy plane enclosed by the
curve C, then we have the following equality between a double integral
over the region and a line integral around the boundary curve
/ / / DQ DP \ /
| | ( -- - -- ) dx dy = | (Qdy + Pdx)
/ / \ Dx Dy / /
R C
where "D" denotes partial derivatives. To show how this reduces to
the simple area formula, notice that if we set Q=x and P=-y then
DQ/Dx = 1 and DP/Dy = -1, and Green's Theorem reduces to
/ / /
| | 2 dx dy = | (xdy - ydx)
/ / /
R C
The left side is twice the area of the enclosed region R, and the
right side is twice our previous formula for the area (with the
opposite sign convention).