On Ptolmey's Theorem
Consider an arbitrary set of six quantities A,B,C,D,E,F that satisfy
the relation
sin(A)sin(B) + sin(C)sin(D) + sin(E)sin(F) = 0 (1)
What restrictions does this place on the values of A though F? Recall
that the exponential form of the sine function is
ix -ix
e - e
sin(x) = ----------
2i
so we can write the preceding sum of products in terms of these
exponentials, expand the products, and multiply through by -4 to
give
(A+B)i (A-B)i -(A-B)i -(A+B)i
e - e - e + e
(C+D)i (C-D)i -(C-D)i -(C+D)i
+ e - e - e + e
+ (E+F)i (E-F)i -(E-F)i -(E+F)i
e - e - e + e = 0
To make this sum vanish, the most direct approach is to equate some
of the exponents, such as by imposing the equalities shown below
A+B = C-D C+D = E-F E+F = A-B
(There are other similar assignments we can make, but it can be shown
that they all lead to the same result.) This implies that
D = -A - B + C E = C - B F = A - C
Substituting into (1) and replacing C with -C, we have the identity
sin(A)sin(B) + sin(C)sin(A+B+C) - sin(A+C)sin(B+C) = 0 (2)
This identity, which applies to any three values A,B,C, is known as
Ptolmey's Theorem, and is usually expressed in terms of a quadri-
lateral inscribed in a circle as illustrated below:
 Recall that the product of the two distances from a point to a circle
along any given line is constant (see Quadrilateral in a Circle), so
in the left-hand figure we have AI*IC = BI*ID, which implies the
similarity of opposing triangles. Also, we know that the angle sub-
tended by a given chord from the center of a circle is twice the angle
subtended from any point on the circumference (see the note on
Loci of Equi-Angular Points), so we can identify the central angles
as shown in the left-hand figure. Obviously the sum of the four
basic angles is a+b+c+d = PI.
The length of a chord subtending a central angle of theta is
L = 2sin(theta/2), so we have the lengths
AB = 2sin(a) BC = 2sin(b) CD = 2sin(d) AD = 2sin(c)
AC = 2sin(a+b) BD = 2sin(b+d)
Since d = PI-(a+b+c) we can replace sin(d) with sin(a+b+c), and we
can replace sin(b+d) with sin(a+c). Now, using the identity (2), we
have
sin(a)sin(a+b+c) + sin(b)sin(c) - sin(a+b)sin(a+c) = 0
which is equivalent to the usual geometric formulation of Ptolmey's
Theorem in terms of the edge lengths and diagonals of a quadrilateral
inscribed in a circle
AB*CD + BC*AD = AC*BD
Of course, there's a well-known and very simple geometric proof of
Ptolmey's Theorem.
Recall that the product of the two distances from a point to a circle
along any given line is constant (see Quadrilateral in a Circle), so
in the left-hand figure we have AI*IC = BI*ID, which implies the
similarity of opposing triangles. Also, we know that the angle sub-
tended by a given chord from the center of a circle is twice the angle
subtended from any point on the circumference (see the note on
Loci of Equi-Angular Points), so we can identify the central angles
as shown in the left-hand figure. Obviously the sum of the four
basic angles is a+b+c+d = PI.
The length of a chord subtending a central angle of theta is
L = 2sin(theta/2), so we have the lengths
AB = 2sin(a) BC = 2sin(b) CD = 2sin(d) AD = 2sin(c)
AC = 2sin(a+b) BD = 2sin(b+d)
Since d = PI-(a+b+c) we can replace sin(d) with sin(a+b+c), and we
can replace sin(b+d) with sin(a+c). Now, using the identity (2), we
have
sin(a)sin(a+b+c) + sin(b)sin(c) - sin(a+b)sin(a+c) = 0
which is equivalent to the usual geometric formulation of Ptolmey's
Theorem in terms of the edge lengths and diagonals of a quadrilateral
inscribed in a circle
AB*CD + BC*AD = AC*BD
Of course, there's a well-known and very simple geometric proof of
Ptolmey's Theorem.
 If we locate the point K along the line AC such that the angle ABK
equals d, then triangle ABK is similar to triangle DBC (as indicated
in the left-hand figure above), so we have AB/AK = DB/DC, and hence
AB*CD = BD*AK. Likewise the triangle BCK is similar to the triangle
BDA, so we get BC/KC = BD/AD and hence BC*AD = BD*KC. Adding these
results together gives
AB*CD + BC*AD = BD*(AK + KC) = AD*AC
This is often specialized to give the addition formulas for the
sine and cosine. For example, if we set C=PI/2 in equation (2), and
recall that sin(PI/2 + x) = cos(x) we have
cos(A+B) = cos(A)cos(B) - sin(A)sin(B)
Still, it's interesting that Ptolmey's Theorem can be seen as arising
more or less uniquely from the attempt to find solutions of the
trigonometric quadratic form (1). Of course, this can also be
inferred directly from the figure, since the length of a chord
subtending a central angle theta is 2sin(theta/2) and so if we let
2a,2b,2c,2d denote the absolute angles of the radials from the
central point O to the vertices A,B,C,D respectively with respect
to the any reference system as shown below
If we locate the point K along the line AC such that the angle ABK
equals d, then triangle ABK is similar to triangle DBC (as indicated
in the left-hand figure above), so we have AB/AK = DB/DC, and hence
AB*CD = BD*AK. Likewise the triangle BCK is similar to the triangle
BDA, so we get BC/KC = BD/AD and hence BC*AD = BD*KC. Adding these
results together gives
AB*CD + BC*AD = BD*(AK + KC) = AD*AC
This is often specialized to give the addition formulas for the
sine and cosine. For example, if we set C=PI/2 in equation (2), and
recall that sin(PI/2 + x) = cos(x) we have
cos(A+B) = cos(A)cos(B) - sin(A)sin(B)
Still, it's interesting that Ptolmey's Theorem can be seen as arising
more or less uniquely from the attempt to find solutions of the
trigonometric quadratic form (1). Of course, this can also be
inferred directly from the figure, since the length of a chord
subtending a central angle theta is 2sin(theta/2) and so if we let
2a,2b,2c,2d denote the absolute angles of the radials from the
central point O to the vertices A,B,C,D respectively with respect
to the any reference system as shown below
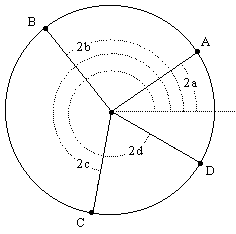 then we have
sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c) = 0
which can be immediately verified using the exponential form.
Naturally there are ways of deducing the usual addition formulas for
the sine and cosine without relying on Ptolmey's Theorem, since the
latter is more general than the former. The simplest algebraic
approach to the addition formulas is just to express the functions
in exponential form and multiply them out. On the other hand, we
also have the very simple geometric proof of the addition formulas
indicated by the figure below:
then we have
sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c) = 0
which can be immediately verified using the exponential form.
Naturally there are ways of deducing the usual addition formulas for
the sine and cosine without relying on Ptolmey's Theorem, since the
latter is more general than the former. The simplest algebraic
approach to the addition formulas is just to express the functions
in exponential form and multiply them out. On the other hand, we
also have the very simple geometric proof of the addition formulas
indicated by the figure below:
 From this perspective, the addition formulas are more or less self-
evident, and we can use them to give another proof of Ptolmey's
Theorem, which is equivalent to the assertion that the function
f(a,b,c,d) = sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c)
vanishes identically, where 2a,2b,2c,2d are an arbitrary (ordered)
set of central angles. If we fix a,c,d we can regard this as a
function f(b) which we can differentiate with respect to b, giving
f'(b) = sin(a-c)cos(b-d) - cos(b-a)sin(d-c) - sin(a-d)cos(b-c)
Now, we know that f(b) vanishes for at least some sets of angles,
such as when the quadrilateral degenerates into a triangle, or when
it is a prefect rectangle. Hence, if we can show that f'(b) vanishes
whenever f(b) vanishes, then it will follow that f(b)=0 for all b,
and by symmetry for all a,b,c,d. To do this, let's first rewrite
f'(b) as follows
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f'(b) = ---------------- - ---------------- - ----------------
tan(b-d) tan(b-a) tan(b-c)
On the assumption that f(b) equals zero for some particular b, we
can divide through f(b) by tan(b-d) to give
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f(b) = ---------------- - ---------------- - ---------------- = 0
tan(b-d) tan(b-d) tan(b-d)
Subtracting this from f'(b) gives
/ 1 1 \
f'(b) = sin(b-a)sin(d-c)( -------- - -------- )
\ tan(b-d) tan(b-a) /
/ 1 1 \
+ sin(a-d)sin(b-c)( -------- - -------- )
\ tan(b-d) tan(b-c) /
Rewriting the tangent functions in terms of sines and cosines gives
/ sin(b-a)cos(b-d) - sin(b-d)cos(b-a) \
f'(b) = sin(b-a)sin(d-c)( ----------------------------------- )
\ sin(b-d) sin(b-a) /
/ sin(b-c)cos(b-d) - sin(b-d)cos(b-c) \
+ sin(a-d)sin(b-c)( ------------------------------------ )
\ sin(b-d) sin(b-c) /
Cancelling sin(b-a) from the first term and sin(b-c) from the second,
and using the addition formula for the sine function that we derived
independently above, this reduces to
sin(d-c)sin(a-d) sin(a-d)sin(c-d)
f'(b) = ---------------- + ----------------
sin(b-d) sin(b-d)
which does indeed equal zero identically. Of course, f"(b) = -f(b),
so this too vanishes identically (as required).
From this perspective, the addition formulas are more or less self-
evident, and we can use them to give another proof of Ptolmey's
Theorem, which is equivalent to the assertion that the function
f(a,b,c,d) = sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c)
vanishes identically, where 2a,2b,2c,2d are an arbitrary (ordered)
set of central angles. If we fix a,c,d we can regard this as a
function f(b) which we can differentiate with respect to b, giving
f'(b) = sin(a-c)cos(b-d) - cos(b-a)sin(d-c) - sin(a-d)cos(b-c)
Now, we know that f(b) vanishes for at least some sets of angles,
such as when the quadrilateral degenerates into a triangle, or when
it is a prefect rectangle. Hence, if we can show that f'(b) vanishes
whenever f(b) vanishes, then it will follow that f(b)=0 for all b,
and by symmetry for all a,b,c,d. To do this, let's first rewrite
f'(b) as follows
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f'(b) = ---------------- - ---------------- - ----------------
tan(b-d) tan(b-a) tan(b-c)
On the assumption that f(b) equals zero for some particular b, we
can divide through f(b) by tan(b-d) to give
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f(b) = ---------------- - ---------------- - ---------------- = 0
tan(b-d) tan(b-d) tan(b-d)
Subtracting this from f'(b) gives
/ 1 1 \
f'(b) = sin(b-a)sin(d-c)( -------- - -------- )
\ tan(b-d) tan(b-a) /
/ 1 1 \
+ sin(a-d)sin(b-c)( -------- - -------- )
\ tan(b-d) tan(b-c) /
Rewriting the tangent functions in terms of sines and cosines gives
/ sin(b-a)cos(b-d) - sin(b-d)cos(b-a) \
f'(b) = sin(b-a)sin(d-c)( ----------------------------------- )
\ sin(b-d) sin(b-a) /
/ sin(b-c)cos(b-d) - sin(b-d)cos(b-c) \
+ sin(a-d)sin(b-c)( ------------------------------------ )
\ sin(b-d) sin(b-c) /
Cancelling sin(b-a) from the first term and sin(b-c) from the second,
and using the addition formula for the sine function that we derived
independently above, this reduces to
sin(d-c)sin(a-d) sin(a-d)sin(c-d)
f'(b) = ---------------- + ----------------
sin(b-d) sin(b-d)
which does indeed equal zero identically. Of course, f"(b) = -f(b),
so this too vanishes identically (as required).
Return to MathPages Main Menu
Сайт управляется системой
uCoz Recall that the product of the two distances from a point to a circle
along any given line is constant (see Quadrilateral in a Circle), so
in the left-hand figure we have AI*IC = BI*ID, which implies the
similarity of opposing triangles. Also, we know that the angle sub-
tended by a given chord from the center of a circle is twice the angle
subtended from any point on the circumference (see the note on
Loci of Equi-Angular Points), so we can identify the central angles
as shown in the left-hand figure. Obviously the sum of the four
basic angles is a+b+c+d = PI.
The length of a chord subtending a central angle of theta is
L = 2sin(theta/2), so we have the lengths
AB = 2sin(a) BC = 2sin(b) CD = 2sin(d) AD = 2sin(c)
AC = 2sin(a+b) BD = 2sin(b+d)
Since d = PI-(a+b+c) we can replace sin(d) with sin(a+b+c), and we
can replace sin(b+d) with sin(a+c). Now, using the identity (2), we
have
sin(a)sin(a+b+c) + sin(b)sin(c) - sin(a+b)sin(a+c) = 0
which is equivalent to the usual geometric formulation of Ptolmey's
Theorem in terms of the edge lengths and diagonals of a quadrilateral
inscribed in a circle
AB*CD + BC*AD = AC*BD
Of course, there's a well-known and very simple geometric proof of
Ptolmey's Theorem.
Recall that the product of the two distances from a point to a circle
along any given line is constant (see Quadrilateral in a Circle), so
in the left-hand figure we have AI*IC = BI*ID, which implies the
similarity of opposing triangles. Also, we know that the angle sub-
tended by a given chord from the center of a circle is twice the angle
subtended from any point on the circumference (see the note on
Loci of Equi-Angular Points), so we can identify the central angles
as shown in the left-hand figure. Obviously the sum of the four
basic angles is a+b+c+d = PI.
The length of a chord subtending a central angle of theta is
L = 2sin(theta/2), so we have the lengths
AB = 2sin(a) BC = 2sin(b) CD = 2sin(d) AD = 2sin(c)
AC = 2sin(a+b) BD = 2sin(b+d)
Since d = PI-(a+b+c) we can replace sin(d) with sin(a+b+c), and we
can replace sin(b+d) with sin(a+c). Now, using the identity (2), we
have
sin(a)sin(a+b+c) + sin(b)sin(c) - sin(a+b)sin(a+c) = 0
which is equivalent to the usual geometric formulation of Ptolmey's
Theorem in terms of the edge lengths and diagonals of a quadrilateral
inscribed in a circle
AB*CD + BC*AD = AC*BD
Of course, there's a well-known and very simple geometric proof of
Ptolmey's Theorem.
 If we locate the point K along the line AC such that the angle ABK
equals d, then triangle ABK is similar to triangle DBC (as indicated
in the left-hand figure above), so we have AB/AK = DB/DC, and hence
AB*CD = BD*AK. Likewise the triangle BCK is similar to the triangle
BDA, so we get BC/KC = BD/AD and hence BC*AD = BD*KC. Adding these
results together gives
AB*CD + BC*AD = BD*(AK + KC) = AD*AC
This is often specialized to give the addition formulas for the
sine and cosine. For example, if we set C=PI/2 in equation (2), and
recall that sin(PI/2 + x) = cos(x) we have
cos(A+B) = cos(A)cos(B) - sin(A)sin(B)
Still, it's interesting that Ptolmey's Theorem can be seen as arising
more or less uniquely from the attempt to find solutions of the
trigonometric quadratic form (1). Of course, this can also be
inferred directly from the figure, since the length of a chord
subtending a central angle theta is 2sin(theta/2) and so if we let
2a,2b,2c,2d denote the absolute angles of the radials from the
central point O to the vertices A,B,C,D respectively with respect
to the any reference system as shown below
If we locate the point K along the line AC such that the angle ABK
equals d, then triangle ABK is similar to triangle DBC (as indicated
in the left-hand figure above), so we have AB/AK = DB/DC, and hence
AB*CD = BD*AK. Likewise the triangle BCK is similar to the triangle
BDA, so we get BC/KC = BD/AD and hence BC*AD = BD*KC. Adding these
results together gives
AB*CD + BC*AD = BD*(AK + KC) = AD*AC
This is often specialized to give the addition formulas for the
sine and cosine. For example, if we set C=PI/2 in equation (2), and
recall that sin(PI/2 + x) = cos(x) we have
cos(A+B) = cos(A)cos(B) - sin(A)sin(B)
Still, it's interesting that Ptolmey's Theorem can be seen as arising
more or less uniquely from the attempt to find solutions of the
trigonometric quadratic form (1). Of course, this can also be
inferred directly from the figure, since the length of a chord
subtending a central angle theta is 2sin(theta/2) and so if we let
2a,2b,2c,2d denote the absolute angles of the radials from the
central point O to the vertices A,B,C,D respectively with respect
to the any reference system as shown below
 then we have
sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c) = 0
which can be immediately verified using the exponential form.
Naturally there are ways of deducing the usual addition formulas for
the sine and cosine without relying on Ptolmey's Theorem, since the
latter is more general than the former. The simplest algebraic
approach to the addition formulas is just to express the functions
in exponential form and multiply them out. On the other hand, we
also have the very simple geometric proof of the addition formulas
indicated by the figure below:
then we have
sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c) = 0
which can be immediately verified using the exponential form.
Naturally there are ways of deducing the usual addition formulas for
the sine and cosine without relying on Ptolmey's Theorem, since the
latter is more general than the former. The simplest algebraic
approach to the addition formulas is just to express the functions
in exponential form and multiply them out. On the other hand, we
also have the very simple geometric proof of the addition formulas
indicated by the figure below:
 From this perspective, the addition formulas are more or less self-
evident, and we can use them to give another proof of Ptolmey's
Theorem, which is equivalent to the assertion that the function
f(a,b,c,d) = sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c)
vanishes identically, where 2a,2b,2c,2d are an arbitrary (ordered)
set of central angles. If we fix a,c,d we can regard this as a
function f(b) which we can differentiate with respect to b, giving
f'(b) = sin(a-c)cos(b-d) - cos(b-a)sin(d-c) - sin(a-d)cos(b-c)
Now, we know that f(b) vanishes for at least some sets of angles,
such as when the quadrilateral degenerates into a triangle, or when
it is a prefect rectangle. Hence, if we can show that f'(b) vanishes
whenever f(b) vanishes, then it will follow that f(b)=0 for all b,
and by symmetry for all a,b,c,d. To do this, let's first rewrite
f'(b) as follows
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f'(b) = ---------------- - ---------------- - ----------------
tan(b-d) tan(b-a) tan(b-c)
On the assumption that f(b) equals zero for some particular b, we
can divide through f(b) by tan(b-d) to give
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f(b) = ---------------- - ---------------- - ---------------- = 0
tan(b-d) tan(b-d) tan(b-d)
Subtracting this from f'(b) gives
/ 1 1 \
f'(b) = sin(b-a)sin(d-c)( -------- - -------- )
\ tan(b-d) tan(b-a) /
/ 1 1 \
+ sin(a-d)sin(b-c)( -------- - -------- )
\ tan(b-d) tan(b-c) /
Rewriting the tangent functions in terms of sines and cosines gives
/ sin(b-a)cos(b-d) - sin(b-d)cos(b-a) \
f'(b) = sin(b-a)sin(d-c)( ----------------------------------- )
\ sin(b-d) sin(b-a) /
/ sin(b-c)cos(b-d) - sin(b-d)cos(b-c) \
+ sin(a-d)sin(b-c)( ------------------------------------ )
\ sin(b-d) sin(b-c) /
Cancelling sin(b-a) from the first term and sin(b-c) from the second,
and using the addition formula for the sine function that we derived
independently above, this reduces to
sin(d-c)sin(a-d) sin(a-d)sin(c-d)
f'(b) = ---------------- + ----------------
sin(b-d) sin(b-d)
which does indeed equal zero identically. Of course, f"(b) = -f(b),
so this too vanishes identically (as required).
From this perspective, the addition formulas are more or less self-
evident, and we can use them to give another proof of Ptolmey's
Theorem, which is equivalent to the assertion that the function
f(a,b,c,d) = sin(a-c)sin(b-d) - sin(b-a)sin(d-c) - sin(a-d)sin(b-c)
vanishes identically, where 2a,2b,2c,2d are an arbitrary (ordered)
set of central angles. If we fix a,c,d we can regard this as a
function f(b) which we can differentiate with respect to b, giving
f'(b) = sin(a-c)cos(b-d) - cos(b-a)sin(d-c) - sin(a-d)cos(b-c)
Now, we know that f(b) vanishes for at least some sets of angles,
such as when the quadrilateral degenerates into a triangle, or when
it is a prefect rectangle. Hence, if we can show that f'(b) vanishes
whenever f(b) vanishes, then it will follow that f(b)=0 for all b,
and by symmetry for all a,b,c,d. To do this, let's first rewrite
f'(b) as follows
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f'(b) = ---------------- - ---------------- - ----------------
tan(b-d) tan(b-a) tan(b-c)
On the assumption that f(b) equals zero for some particular b, we
can divide through f(b) by tan(b-d) to give
sin(a-c)sin(b-d) sin(b-a)sin(d-c) sin(a-d)sin(b-c)
f(b) = ---------------- - ---------------- - ---------------- = 0
tan(b-d) tan(b-d) tan(b-d)
Subtracting this from f'(b) gives
/ 1 1 \
f'(b) = sin(b-a)sin(d-c)( -------- - -------- )
\ tan(b-d) tan(b-a) /
/ 1 1 \
+ sin(a-d)sin(b-c)( -------- - -------- )
\ tan(b-d) tan(b-c) /
Rewriting the tangent functions in terms of sines and cosines gives
/ sin(b-a)cos(b-d) - sin(b-d)cos(b-a) \
f'(b) = sin(b-a)sin(d-c)( ----------------------------------- )
\ sin(b-d) sin(b-a) /
/ sin(b-c)cos(b-d) - sin(b-d)cos(b-c) \
+ sin(a-d)sin(b-c)( ------------------------------------ )
\ sin(b-d) sin(b-c) /
Cancelling sin(b-a) from the first term and sin(b-c) from the second,
and using the addition formula for the sine function that we derived
independently above, this reduces to
sin(d-c)sin(a-d) sin(a-d)sin(c-d)
f'(b) = ---------------- + ----------------
sin(b-d) sin(b-d)
which does indeed equal zero identically. Of course, f"(b) = -f(b),
so this too vanishes identically (as required).