The Limit Paradox

There is an interesting "thought experiment" that often puzzles 
students when they first learn about limits in calculus.  This is 
known as the Limit Paradox, and is sometimes presented in the 
form of an equalateral triangle as shown below:
           
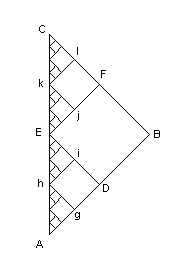Assuming this is an equilaterial triangle, the path ABC is twice 
as long as AC.  Similarly the path ADEFC is also twice as long as 
AC, as is the path AghiEjklC, and so on.  Breaking down the jagged 
path into smaller and smaller jags, the deviation of the jaged path
from the straight line AC goes to zero, so, in a sense, the line AC 
is the "limit" of the sequence of jagged paths.  This might seem to
suggest that the length of AC is twice the length of itself!

Paradoxes like this were discussed extensively (and very seriously) 
during the early history of calculus.  Another example - one that 
may help to illustrate the fallacy of these paradoxes - is to consider 
the sequence of numbers 0.9, 0.99, 0.999, etc.  Clearly none of these 
numbers is an integer.  However, these numbers approach ever more 
closely the number 1.0, so are we justified in concluding that the
number 1.0 is not an integer?  No.  Similarly, we could note that 
the average size of the non-zero decimal digits of 0.9, 0.99, etc 
is 9, so we might think the average size of the non-zero digits of 
1.0 must also be 9, but of course it isn't.

In the words of The Encyclopedia Britanica,

   "The limit paradox is the result of the mistaken idea 
    that the limiting configuration must have properties 
    which are the limiting cases of the corresponding 
    properties of the approximating configurations."

While I wouldn't cite this as a model of didactic clarity, it does
make the key point, which is that entities in any given sequence 
generally possess multiple properties, and an entity that possesses 
the limiting value of one of those properties doesn't necessarily 
possess the limiting value of ALL those properties (many of which
may not even converge).

In the case of the jagged paths, we are actually considering the 
boundaries of the minimal envelope surrounding the path, and noting 
that the limiting jagged path resides entirely within an arbitrarily 
small envelope around the line AC.  The boundaries of this envelope 
approach the line AC, in position as well as length, but the length 
of the jagged line within this envelope does not converge on the 
length of the envelope containing it.  In fact, we could easily 
construct a sequence of looping paths, with an exponentially 
increasing number of geometrically decreasing loops, such that 
the total length of the looping path from A to C goes to infinity 
as the envelope converges on the straight line AC.

These examples illustrate that you have to be careful about which 
property is being taken to the limit.  It's worthwhile to keep this 
in mind when considering things like Koch's snowflake and other 
fractal boundaries, which tend to be defined as the limiting cases 
of progressive fragmentation processes.  Those constructions are 
more complicated and involve more subtle issues, because the minimal 
envelope itself becomes progressively more convoluted, in contrast 
to the simple "limit paradox" we've been considering, where the 
limiting envelope is well-behaved.