Thinking Outside the Triangle

Given an arbitrary triangle ABC, let D be the foot of the perpendicular
from A to BC, let E be the foot of the perpendicular from D to AC, and 
let F be a point on the line DE, as illustrated below

        

Florin Pirvanescu challenged the readers of Mathematics Magazine in
June 1991 to prove that AF is perpendicular to BE if and only if 
FE/FD = BD/DC.  Several proofs have appeared, based on synthetic,
projective, and vector methods.  These proofs are all fairly elaborate,
but there is actually a very simple elementary proof, which is a nice
example of "thinking outside the box".

Let G be the foot of the perpendicular from B to DE, as shown below.

        

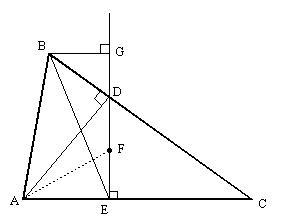Clearly BDG ~ DAE and DGE ~ DBC, so we have BG/DG = DE/AE and 
EG/DG = CB/DB.  Also, AEF ~ EGB, giving EG/BG = AE/FE, if and only 
if AF is perpendicular to BE.  Thus we have

                 /BG\  /EG\       /DE\  /AE\
                ( -- )( -- )  =  ( -- )( -- )
                 \DG/  \BG/       \AE/  \FE/

which implies DE/FE = EG/DG = CB/DB and so FED ~ DBC if and only if
AF is perpendicular to BE.