Appendix B: Nth Order Recurrence Formulas

In Sections 2 and 3 of this document the optimum recurrence formulas for first and second order response were derived based on the assumption that the input function x(t) was the first or second-degree polynomial (respectively) that passes through the given discrete values of x(t). In this appendix we generalize this method to Nth order response.

Let x(t) and y(t) denote continuous functions of time, related according to the Nth order differential equation

where the coefficients a_k and b_k are constants. We will denote by r₁, r₂,..., r_N the roots of the characteristic polynomial of the left hand side of this differential equation.

For some instant t₀ we are given the discrete values x(t₀), x(t₀+Dt), x(t₀+2Dt), ..., x(t₀+NDt) and y(t₀), y(t₀+Dt), y(t₀+2Dt), ..., y(t₀+(N-1)Dt) , where Dt is the execution interval of the simulation. For brevity we will denote y(t₀+kDt) by y_k and x(t₀+kDt) by x_k. Our objective is to determine the value of y_N based on the assumption that the function x(t) over the time interval from t₀ to t₀+NDt is identical to the Nth degree polynomial that passes through the given discrete values of x(t).

Define the N� 1 column vector Y and the (N+1)� 1 column vector X as follows:

Then define the square (N+1) � (N+1) matrices A, B, and T such that the elements in the jth columns of the ith rows are as follows

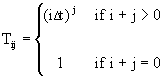
where i and j range from 0 to N. Then define the 1 � (N+1) and 1 � N row vectors

S = [ s_N s_N-1 ... s₁ 1 ]s = [ s_N s_N-1 ... s₁ ]

where s_k denotes (-1)^k times the kth elementary symmetric function of the quantities , i=1,2,..,N. For example, if N=3 we have

In terms of the matrices defined above, the value of y_N can now be expressed as

y_N = -sY + STA^-1BT^-1X

Letting g_i denote the ith element of the row vector given by STA^-1BT^-1, we have the explicit recurrence formula

y_n = s₁ y_n-1 - s₂ y_n-2 - ... - s_N y_n-N + g_N+1 x_n + g_N x_n-1 + ... + g₁ x_n-N

The values of s_k are always purely real for real coefficients a_k, even when the roots r₁,r₂,.., r_N are complex. Also, for reasons discussed in Section 2.2.5, the values of s_k are the exact y-term coefficients, regardless of how the x(t) function is interpolated. Only the gk coefficients would be affected if we changed our assumption as to the form of x(t) (that is, if we identified x(t) with a function different from the Nth order polynomial fit through the discrete values).

One way of computing s_k is to solve the characteristic equation

a_N z^N + a_N-1 z^N-1 + ... + a₁ z + a₀ = 0

for all the roots r_j, j=1 to N, and then directly compute the symmetric functions of the exponentials. However, finding all the (complex) roots of an Nth degree polynomial can be computationally laborious and involves numerous special cases. Another approach, one that avoids having to explicitly determine all the roots of the characteristic polynomial, is to use "Newton's sums". For any non-negative integer k, let w(k) denote the sum of the kth powers of the roots r₁,r₂,..,r_N. Clearly w(0) = N. The values of w(k) for k=1,2,... can be found using the identities

a_N w(1) + 1a_N-1 = 0

a_N w(2) + a_N-1 w(1) + 2a_N-2 = 0

a_N w(3) + a_N-1 w(2) + a_N-2 w(1) + 3a_N-3 = 0

for k < N, and the recurrence

a_N w(k) + a_N-1 w(k-1) + ... + a₀ w(k-N) = 0

for all k � N. Now let E(k) denote the sum of the kth powers of the values of , i=1,2,..,N. The Taylor series expansion gives

The values of s_k can now be computed using the identities

E(1) + 1s₁ = 0

E(2) + s₁ E(1) + 2s₂ = 0

E(3) + s₁ E(2) + s₂ E(1) + 3s₃ = 0

etc.