Is there necessarily just a single "Hubble relation"? According to the conventional view of the universe as a coherent manifold, and assuming homogeneity, the answer is clearly yes, but can we be sure that the separations between objects in the universe constitute a coherent manifold? It's very tempting to assume that ordinary metrical relations such as the triangle inequality must apply to all the separations in the universe, on all scales, but what evidence do we really have to support such assumptions? It's worth remembering that even our local spacetime fails to satisfy the axioms of a metric, including the triangle inequality.
According to the conventional Robertson-Walker cosmology the scale parameter R of the universe satisfies the freefall equations of motion that we've discussed in previous sections. Depending on the initial conditions this will either be a cycloid (for a closed finite universe) or an open ended curve for an open infinite universe. According to these models we expect all the large-scale separations in the universe to follow basically the same functions of cosmological time (which tends to roughly correspond to local proper time, since most objects have relatively low velocities with respect to the local frame in which the cosmic background radiation is isotropic). We've seen that these two classes of separations (along with general co-inertial separations and rotating separations) are solutions of the differential equation
![]()
However, the equation also has other solutions besides the cycloidal and co-inertial, etc. For example, it is satisfied by sinusoidal functions and exponential functions. This raises the question of whether there might be a class of exponential cosmological distances in addition to the cycloidal distances.
An alternative view is to regard separations as the elementary objects of nature. According to this view, the "particles" that we deal with consciously are really just convenient ways of psychologically organizing our information about separations, and we mentally "arrange" the local separations in such a way that they satisfy the requirements of a 3-dimensional manifold. (It's an interesting abstract exercise to consider the number of distinct "point configurations" that can be construed from a given multi-set of distances.)
Several other categories of naturally occurring physical separations also satisfy the separation equation. For example, if you place a mass on a frictionless slider and rotate the slider with constant angular velocity, the separation of the mass from the center of rotation satisfies the "separation equation".
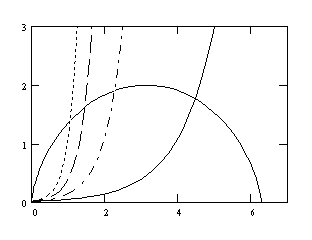
This leads to speculation that the universe may contain separations that satisfy the above equation for other values of N besides 2 and 3. With N = 2 the equation describes the cycloid characteristic of the "standard model" of the universe's expansion, giving a roughly linear relation between distance and recession velocity at the present time. However, with other values of N we can have other classes of solutions. In particular, with N = - 1 we have a class of exponential solutions. To check this theory, astronomers should look for objects that are highly redshifted but much closer to us than the standard Hubble model would suggest. Of course, even if this view was correct, it might be the case that all the exponential separations have already passed out of view.
The possibility of surprises in this area was highlighted in 1998 when two independent teams of astronomers reported data that seems to indicate the expansion of the universe is actually accelerating, rather than slowing down as predicted by the standard GR model with zero cosmological constant. These findings have raised again the old idea that the cosmological constant (which Einstein at one point called his biggest blunder) may be significantly non-zero. On the other hand, the above discussion shows that the idea of at least some cosmological separations increasing at an accelerating rate can arise from completely a priori considerations. Of course, as long as a single coherent expansion model is adequate to explain our observations, the standard GR models of a smooth manifold will remain viable. Less conventional notions such as those discussed above would only be called for if we begin to see conflicting evidence, e.g., if some observations strongly indicate accelerating expansion while others strongly indicate decelerating expansion.