According to Newton's theory the acceleration of gravity of a test particle at a given radial distance from a large mass is invariant, so it may seem slightly surprising that in general relativity the second derivative of the coordinate radial parameter r with respect to the coordinate time parameter t for a particle in a radial orbit in Schwarzschild geometry depends not only on the spacetime location of the particle (i.e., r and t) but also on the trajectory of the particle through that point. To derive d2r/dt2, recall from Section 6.4 that
![]()
where t is the proper time of the radially "orbiting" particle. This corresponds to the well-known cycloidal parametric relations between r and t:
![]()
![]()
![]()
![]()
where R is the "top" of the orbit and w is an angular parameter that ranges from 0 at the top of the orbit (r = R) to p at the bottom (r = 0). So a plot of r versus t can be drawn by tracing the motion of a point on the rim of a wheel as it rolls along a flat surface. (This same relation applies in Newtonian gravity if we replace t with t.) Now, differentiating these parametric equations with respect to w gives
![]()
![]()
![]()
![]()
Therefore we have
![]()
From the parametric equation for r we have
![]()
Denoting this quantity by "u", this implies that
![]()
Solving this for tan(w/2) gives
![]()
We want w = 0 at r = R so we choose the first root and substitute into the preceding equation for dr/dt to give
![]()
In addition, we have the derivative of coordinate time with respect to proper time of the particle
![]()
(See Section 6.5 for a derivation of this relation from the basic geodesic equations.) Dividing dr/dt by dt/dt gives
![]()
Now let's return to our original equation
![]()
Multiplying and dividing the left side by dt/dt gives
![]()
Writing dr/dt as the product of dr/dt and dt/dt and evaluating the derivative with respect to t gives
![]()
Recalling that we have an expression for dt/dt as a function of r, we multiply and divide the derivative of dt/dt with respect to t by (dr/dt) to give
![]()
The derivative of dt/dt with respect to r is
![]()
so we have everything we need to solve the preceding equation for d2r/dt2, giving the result
![]()
As expected, this reduces to
![]()
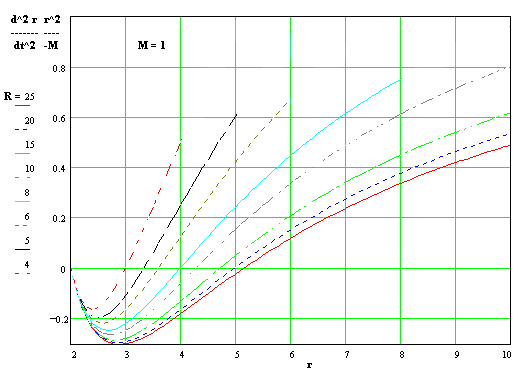
at the apogee when r = R. Also, notice that d2r/dt2 is negative initially, meaning that dr/dt is becoming more negative, but eventually it passes through an inflection point and then d2r/dt2 becomes positive, meaning that the particle is actually decelerating as dr/dt goes to zero at r = 2M. The shape of this curve at a given radial position r depends on the trajectory of the particle as it passes through that radial location, which depends on the energy of the orbit (i.e., the apogee R). In particular, notice that the radial position
![]()
at which r'' changes from negative to positive depends on the apogee R of the orbit, although if R is much larger than M (as is typically the case) the inflection point will be approximately 6M. A plot of d2r/dt2 divided by -M/r2 for various values of R is shown below: