Is e Normal?
A number is called "normal" with respect to a given base if, when
the number is expressed in that base, the asymptotic frequencies of
occurrence of each distinct string of k digits are equal, and this
applies to every positive integer k. For example, if a number is
normal in the base 10, the asymptotic frequency of occurrence of
each of the decimal numerals 0,1,..,9 is precisely 1/10, and the
asymptotic frequency of each two-digit strings 00,01,02,...,99 is
exactly 1/100, and so on.
By the same token, the asymptotic frequency of occurrence of each
10-digit string must be exactly 1/10^10. Of the distinct 10-digit
strings, exactly 10! contain each numeral just once, i.e., there are
10! permutations of the 10 decimal numerals 0,1,..,9. Therefore, if
a number is normal in the base 10, the asymptotic frequency of 10-
digit strings comprising permutations of all 10 numerals must be
10!/10^10, which equals roughly 1 / 2755.73.
It is widely believed that the two most naturally occurring
transcendental numbers, pi and e, are both normal in the base 10
(although it has never even been proved that the individual numerals
of these numbers have equal asymptotic frequencies), and indeed if
we examine the occurrences of complete permutation strings in the
first million digits of pi we find very good agreement with the
expected frequency, i.e., if p(n) denotes the numbers of complete
permutation strings in the first n digits, then n/p(n) apparently
converges on 2755.
However, if we examine the first million decimal digits of the number
e, we find that the ratio n/p(n) seems to settle at a value around
2520. This is illustrated in the figure below.
 This result is confirmed by continuing to check the next million
digits, which show no particular upward trend in this ratio, and
leave it at 2568. (The value for the first TWO million digits of
e are presented in The e in Petersburg.) Hence the frequency
of complete permutation strings is more than 6% greater than what
would be predicted for a "normal" number.
This evidence of non-normality seems hard to believe, so I checked
digits of e computed independently by two different sources, but in
both cases the results were identical. Also, the fact that the digits
of pi yield the expected frequency using my counting program tends to
support the validity of the program - which, after all, is just a
simple counting routine. Is there some systematic error in this
assessment, or can we say that e is definitely NOT normal?
To provide another check of these results I acquired a set of 1 million
pseudo-random digits generated by the Rand Corporation in 1955 based
on work begun in 1947. According to the documentation accompanying
these digits, the basic table was produced during May and June of 1947
by means of an "electronic roulette wheel". This device consisted of a
random frequency pulse source, providing on the average about 100,000
pulses per second, gated about once per second by a constant frequency
pulse. The pulses were then passed through a 5-place binary counter.
There were about 3000 revolutions per "trial", leading to the output
of one number per second. A binary-to-decimal converter was then used
to convert 20 of the 32 numbers (the other twelve were discarded), and
it retained only the final digit of two-digit numbers.
Interestingly, the documentation notes that "production from the
original machine showed statistically significant biases, and the
engineers had to make several modifications and refinements of the
circuits before production of apparently satisfactory numbers was
achieved". Even after these modification, some some statistical
biases remained. The final step in producing the table of "random
digits" was to transform the table by adding pairs of digits modulo
10. This was done "in order to improve the distribution of the
digits". There were 20,000 punched cards with 50 digits per
card; each digit on a given card was added modulo 10 to the
corresponding digit of the preceding card to yield a rerandomized
digit. It is this transformed table which is published..."
This is an interesting "re-randomization" technique, since it
represents something like a convolution of the data sequence. In
other words, if the string of digits is in an array D[i] of length
1 million, the process consisted of applying the transformation
D'[i] = (D[i] + D[i-50]) mod 10
Presumably for completeness we would stipulate that the digits "wrap
around", e.g., D'[1] would equal the sum of D[1] and D[999951].
Iterations of this transformation doesn't seem to degenerate into
an orderly sequence, given a sufficiently disordered initial sequence.
In any case, results for the Rand sequence are also plotted on the
figure above, labeled as "synthesized". This sequence behaves very
differently than the digits of pi or e. It starts out quite high,
meaning that there is a scarcity of complete permutation sequences.
Eventually it settles down in the vicinity of the theoretical value,
but it seem to converge on a slightly higher value. Is there a
systematic bias in the Rand data, or does it simply require far more
digits to establish the asymptotic density of complete permutation
sequences?
To study this further, I acquired the first two million decimal digits
of the square root of 2, as computed by Nemiroff & Bonnell. The rate
of occurrence of complete permutation strings is shown in the figure
below.
This result is confirmed by continuing to check the next million
digits, which show no particular upward trend in this ratio, and
leave it at 2568. (The value for the first TWO million digits of
e are presented in The e in Petersburg.) Hence the frequency
of complete permutation strings is more than 6% greater than what
would be predicted for a "normal" number.
This evidence of non-normality seems hard to believe, so I checked
digits of e computed independently by two different sources, but in
both cases the results were identical. Also, the fact that the digits
of pi yield the expected frequency using my counting program tends to
support the validity of the program - which, after all, is just a
simple counting routine. Is there some systematic error in this
assessment, or can we say that e is definitely NOT normal?
To provide another check of these results I acquired a set of 1 million
pseudo-random digits generated by the Rand Corporation in 1955 based
on work begun in 1947. According to the documentation accompanying
these digits, the basic table was produced during May and June of 1947
by means of an "electronic roulette wheel". This device consisted of a
random frequency pulse source, providing on the average about 100,000
pulses per second, gated about once per second by a constant frequency
pulse. The pulses were then passed through a 5-place binary counter.
There were about 3000 revolutions per "trial", leading to the output
of one number per second. A binary-to-decimal converter was then used
to convert 20 of the 32 numbers (the other twelve were discarded), and
it retained only the final digit of two-digit numbers.
Interestingly, the documentation notes that "production from the
original machine showed statistically significant biases, and the
engineers had to make several modifications and refinements of the
circuits before production of apparently satisfactory numbers was
achieved". Even after these modification, some some statistical
biases remained. The final step in producing the table of "random
digits" was to transform the table by adding pairs of digits modulo
10. This was done "in order to improve the distribution of the
digits". There were 20,000 punched cards with 50 digits per
card; each digit on a given card was added modulo 10 to the
corresponding digit of the preceding card to yield a rerandomized
digit. It is this transformed table which is published..."
This is an interesting "re-randomization" technique, since it
represents something like a convolution of the data sequence. In
other words, if the string of digits is in an array D[i] of length
1 million, the process consisted of applying the transformation
D'[i] = (D[i] + D[i-50]) mod 10
Presumably for completeness we would stipulate that the digits "wrap
around", e.g., D'[1] would equal the sum of D[1] and D[999951].
Iterations of this transformation doesn't seem to degenerate into
an orderly sequence, given a sufficiently disordered initial sequence.
In any case, results for the Rand sequence are also plotted on the
figure above, labeled as "synthesized". This sequence behaves very
differently than the digits of pi or e. It starts out quite high,
meaning that there is a scarcity of complete permutation sequences.
Eventually it settles down in the vicinity of the theoretical value,
but it seem to converge on a slightly higher value. Is there a
systematic bias in the Rand data, or does it simply require far more
digits to establish the asymptotic density of complete permutation
sequences?
To study this further, I acquired the first two million decimal digits
of the square root of 2, as computed by Nemiroff & Bonnell. The rate
of occurrence of complete permutation strings is shown in the figure
below.
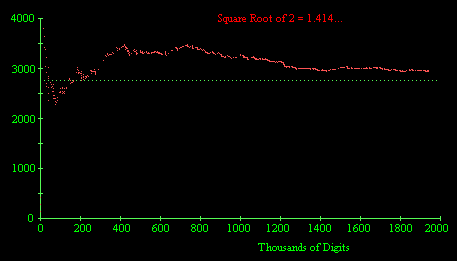 This seems to show a systematic upward bias, i.e., a scarcity of
complete permutation strings relative to the expected frequency based
on the assumption of normality. I also acquired the first million
decimal digits of the square root of 7, and of Euler's constant
gamma = 0.577... The behaviors of n/p(n) for the digits of these
two numbers are shown below.
This seems to show a systematic upward bias, i.e., a scarcity of
complete permutation strings relative to the expected frequency based
on the assumption of normality. I also acquired the first million
decimal digits of the square root of 7, and of Euler's constant
gamma = 0.577... The behaviors of n/p(n) for the digits of these
two numbers are shown below.

 The digits of the square root of 7 seem to converge fairly well on the
predicted frequency, but the digits of gamma seem to be consistently
richer in complete permutations, i.e., n/p(n) is low, at least out to
one million digits.
It may be worth noting that of all these numbers, the digits of pi
are the most thoroughly checked and verified, and those are the digits
that converge most satisfactorily to the theoretical value. For the
digits of the other constants (e, gamma, sqrt(2), sqrt(7)), Nemiroff
& Bonnell are careful to point out that they do NOT guarantee their
accuracy, and they invite other people to check them.
For another check, I acquired the first five million decimal digits
of the square root of 5 as computed by Dawson Merrill. He has actually
computed 10 million digits, but says only the first five million have
been checked, and he is confident of their correctness. The average
interval between complete permutation strings, plotted below, seems to
converge fairly well on the predicted theoretical value.
The digits of the square root of 7 seem to converge fairly well on the
predicted frequency, but the digits of gamma seem to be consistently
richer in complete permutations, i.e., n/p(n) is low, at least out to
one million digits.
It may be worth noting that of all these numbers, the digits of pi
are the most thoroughly checked and verified, and those are the digits
that converge most satisfactorily to the theoretical value. For the
digits of the other constants (e, gamma, sqrt(2), sqrt(7)), Nemiroff
& Bonnell are careful to point out that they do NOT guarantee their
accuracy, and they invite other people to check them.
For another check, I acquired the first five million decimal digits
of the square root of 5 as computed by Dawson Merrill. He has actually
computed 10 million digits, but says only the first five million have
been checked, and he is confident of their correctness. The average
interval between complete permutation strings, plotted below, seems to
converge fairly well on the predicted theoretical value.
 In any case, this raises the question of how many digits would need
to be checked in order to reasonably expect the overall frequency of
complete permutation strings to be within, say, 1% of the theoretical
asymptotic value. Also, does the speed of convergence for the digits
of a particular number have any significance. In particular, is it
significant that the decimal digits of pi evidently converge on the
asymptotic value much sooner than the digits of other irrational
numbers?
One possible way of trying to answer these questions would be to
treat the occurrence of Complete Permutation Strings (CPSs) as a
Poisson process. Of course, since the digits of overlapping strings
are not independent, this isn't exactly correct, because a Poisson
model assumes a memoryless process, i.e., it assumes that the
expected distance to the next occurrence is independent of any
prior occurrences. With CPSs this is not the case, because the
string immediately following a CPS has a probability of about 1/10
of also being a CPS (since the new digit simply needs to equal the
digit being discarded). This is roughly born out in the case of
the digits of e, because of the 778 CPSs there are 67 cases of
consecutive CPSs. There are also 6 cases of two CPSs at a distance
of 2 digits. On the other hand, it's also true that non-CPSs are
disproportionately likely to have non-CPS neighbors, because pairs
of duplicate digits are likely to be contained in the overlap of
neighboring strings.
Nevertheless, we can use the Poisson model to give a rough estimate
of the probability that the observed frequency over a given interval
differs from the asymptotic frequency by various amounts. As
discussed in Poisson Processes and Queues, the probability of
exactly k occurrences of an (exponentially distributed) event with
rate L in time (or number of trials) T is
k
(LT) -LT
P(k) = ------ e
k!
For large k we can use Stirling's formula for k! to write this in
the more easily computed form
_ _
| (k-LT)/k | k
1 | LT e |
P(k) = ------------ | ------------- |
sqrt(2k pi) |_ k _|
We examined the first T = 2,000,000 strings in the decimal expansion
of e, and found k = 778 complete permutation strings. The theoretical
rate is L = 1/2755.73, so the expected number of CPSs in this range
is LT = 725.76. The probability of finding exactly k complete strings
in the first 2 million decimal digits is shown below for k ranging
from 600 to 900.
In any case, this raises the question of how many digits would need
to be checked in order to reasonably expect the overall frequency of
complete permutation strings to be within, say, 1% of the theoretical
asymptotic value. Also, does the speed of convergence for the digits
of a particular number have any significance. In particular, is it
significant that the decimal digits of pi evidently converge on the
asymptotic value much sooner than the digits of other irrational
numbers?
One possible way of trying to answer these questions would be to
treat the occurrence of Complete Permutation Strings (CPSs) as a
Poisson process. Of course, since the digits of overlapping strings
are not independent, this isn't exactly correct, because a Poisson
model assumes a memoryless process, i.e., it assumes that the
expected distance to the next occurrence is independent of any
prior occurrences. With CPSs this is not the case, because the
string immediately following a CPS has a probability of about 1/10
of also being a CPS (since the new digit simply needs to equal the
digit being discarded). This is roughly born out in the case of
the digits of e, because of the 778 CPSs there are 67 cases of
consecutive CPSs. There are also 6 cases of two CPSs at a distance
of 2 digits. On the other hand, it's also true that non-CPSs are
disproportionately likely to have non-CPS neighbors, because pairs
of duplicate digits are likely to be contained in the overlap of
neighboring strings.
Nevertheless, we can use the Poisson model to give a rough estimate
of the probability that the observed frequency over a given interval
differs from the asymptotic frequency by various amounts. As
discussed in Poisson Processes and Queues, the probability of
exactly k occurrences of an (exponentially distributed) event with
rate L in time (or number of trials) T is
k
(LT) -LT
P(k) = ------ e
k!
For large k we can use Stirling's formula for k! to write this in
the more easily computed form
_ _
| (k-LT)/k | k
1 | LT e |
P(k) = ------------ | ------------- |
sqrt(2k pi) |_ k _|
We examined the first T = 2,000,000 strings in the decimal expansion
of e, and found k = 778 complete permutation strings. The theoretical
rate is L = 1/2755.73, so the expected number of CPSs in this range
is LT = 725.76. The probability of finding exactly k complete strings
in the first 2 million decimal digits is shown below for k ranging
from 600 to 900.
 We've also marked on this figure the value 778, which is the number
of CPSs found in the first 2,000,000 decimal digits of e. The
probability that k would be equal to or greater than 778 is only
about 2.8% based on this Poisson model.
A better method of evaluation would be to examine the digits in
disjoint blocks of 10, because these blocks would (presumably) be
statistically independent. On this basis our 2 million digits of e
represent only 200,000 independent samples, among which we would
expect to find 72.57 complete permutation strings. Now, we can
split up the digits in essentially 10 different ways, depending on
how we choose to frame the blocks. This amounts to partitioning
the 778 CPSs according to the least significant digit of their
index. Doing this, we find the following results
index CPSs
----- ------
0 87
1 71
2 80
3 74
4 82
5 76
6 81
7 68
8 85
9 74
On this basis the Poisson model is actually valid, so we can plot
these results on top of the predicted distribution as shown below.
We've also marked on this figure the value 778, which is the number
of CPSs found in the first 2,000,000 decimal digits of e. The
probability that k would be equal to or greater than 778 is only
about 2.8% based on this Poisson model.
A better method of evaluation would be to examine the digits in
disjoint blocks of 10, because these blocks would (presumably) be
statistically independent. On this basis our 2 million digits of e
represent only 200,000 independent samples, among which we would
expect to find 72.57 complete permutation strings. Now, we can
split up the digits in essentially 10 different ways, depending on
how we choose to frame the blocks. This amounts to partitioning
the 778 CPSs according to the least significant digit of their
index. Doing this, we find the following results
index CPSs
----- ------
0 87
1 71
2 80
3 74
4 82
5 76
6 81
7 68
8 85
9 74
On this basis the Poisson model is actually valid, so we can plot
these results on top of the predicted distribution as shown below.
 The average of our ten "samples" is 77.8 (although these samples are
not independent), and we can compute that the probability of this
being 78 or higher is about 27.8%. Hence it is not terribly improbable
that we would find this deviation from the expected number of CPSs
over this number of digits. It would evidently be necessary to
examine about 20 million digits to give a valid basis for drawing
a conclusion about the actual density of CPSs in the decimal digits
of e.
It's interesting that the block indices seem to bifurcate into the
odds and the evens. In fact, if we just focused on the odd blocks,
we find a mean of 72.6 CPSs per 200,000 samples, in excellent
agreement with the expected number (72.57). In contrast, the even-
indexed blocks have an average of 83 CPSs per 200,000 samples. The
probability of finding 83 or more CPSs in this range is only 12.3%.
The average of our ten "samples" is 77.8 (although these samples are
not independent), and we can compute that the probability of this
being 78 or higher is about 27.8%. Hence it is not terribly improbable
that we would find this deviation from the expected number of CPSs
over this number of digits. It would evidently be necessary to
examine about 20 million digits to give a valid basis for drawing
a conclusion about the actual density of CPSs in the decimal digits
of e.
It's interesting that the block indices seem to bifurcate into the
odds and the evens. In fact, if we just focused on the odd blocks,
we find a mean of 72.6 CPSs per 200,000 samples, in excellent
agreement with the expected number (72.57). In contrast, the even-
indexed blocks have an average of 83 CPSs per 200,000 samples. The
probability of finding 83 or more CPSs in this range is only 12.3%.
Return to MathPages Main Menu
Сайт управляется системой
uCoz This result is confirmed by continuing to check the next million
digits, which show no particular upward trend in this ratio, and
leave it at 2568. (The value for the first TWO million digits of
e are presented in The e in Petersburg.) Hence the frequency
of complete permutation strings is more than 6% greater than what
would be predicted for a "normal" number.
This evidence of non-normality seems hard to believe, so I checked
digits of e computed independently by two different sources, but in
both cases the results were identical. Also, the fact that the digits
of pi yield the expected frequency using my counting program tends to
support the validity of the program - which, after all, is just a
simple counting routine. Is there some systematic error in this
assessment, or can we say that e is definitely NOT normal?
To provide another check of these results I acquired a set of 1 million
pseudo-random digits generated by the Rand Corporation in 1955 based
on work begun in 1947. According to the documentation accompanying
these digits, the basic table was produced during May and June of 1947
by means of an "electronic roulette wheel". This device consisted of a
random frequency pulse source, providing on the average about 100,000
pulses per second, gated about once per second by a constant frequency
pulse. The pulses were then passed through a 5-place binary counter.
There were about 3000 revolutions per "trial", leading to the output
of one number per second. A binary-to-decimal converter was then used
to convert 20 of the 32 numbers (the other twelve were discarded), and
it retained only the final digit of two-digit numbers.
Interestingly, the documentation notes that "production from the
original machine showed statistically significant biases, and the
engineers had to make several modifications and refinements of the
circuits before production of apparently satisfactory numbers was
achieved". Even after these modification, some some statistical
biases remained. The final step in producing the table of "random
digits" was to transform the table by adding pairs of digits modulo
10. This was done "in order to improve the distribution of the
digits". There were 20,000 punched cards with 50 digits per
card; each digit on a given card was added modulo 10 to the
corresponding digit of the preceding card to yield a rerandomized
digit. It is this transformed table which is published..."
This is an interesting "re-randomization" technique, since it
represents something like a convolution of the data sequence. In
other words, if the string of digits is in an array D[i] of length
1 million, the process consisted of applying the transformation
D'[i] = (D[i] + D[i-50]) mod 10
Presumably for completeness we would stipulate that the digits "wrap
around", e.g., D'[1] would equal the sum of D[1] and D[999951].
Iterations of this transformation doesn't seem to degenerate into
an orderly sequence, given a sufficiently disordered initial sequence.
In any case, results for the Rand sequence are also plotted on the
figure above, labeled as "synthesized". This sequence behaves very
differently than the digits of pi or e. It starts out quite high,
meaning that there is a scarcity of complete permutation sequences.
Eventually it settles down in the vicinity of the theoretical value,
but it seem to converge on a slightly higher value. Is there a
systematic bias in the Rand data, or does it simply require far more
digits to establish the asymptotic density of complete permutation
sequences?
To study this further, I acquired the first two million decimal digits
of the square root of 2, as computed by Nemiroff & Bonnell. The rate
of occurrence of complete permutation strings is shown in the figure
below.
This result is confirmed by continuing to check the next million
digits, which show no particular upward trend in this ratio, and
leave it at 2568. (The value for the first TWO million digits of
e are presented in The e in Petersburg.) Hence the frequency
of complete permutation strings is more than 6% greater than what
would be predicted for a "normal" number.
This evidence of non-normality seems hard to believe, so I checked
digits of e computed independently by two different sources, but in
both cases the results were identical. Also, the fact that the digits
of pi yield the expected frequency using my counting program tends to
support the validity of the program - which, after all, is just a
simple counting routine. Is there some systematic error in this
assessment, or can we say that e is definitely NOT normal?
To provide another check of these results I acquired a set of 1 million
pseudo-random digits generated by the Rand Corporation in 1955 based
on work begun in 1947. According to the documentation accompanying
these digits, the basic table was produced during May and June of 1947
by means of an "electronic roulette wheel". This device consisted of a
random frequency pulse source, providing on the average about 100,000
pulses per second, gated about once per second by a constant frequency
pulse. The pulses were then passed through a 5-place binary counter.
There were about 3000 revolutions per "trial", leading to the output
of one number per second. A binary-to-decimal converter was then used
to convert 20 of the 32 numbers (the other twelve were discarded), and
it retained only the final digit of two-digit numbers.
Interestingly, the documentation notes that "production from the
original machine showed statistically significant biases, and the
engineers had to make several modifications and refinements of the
circuits before production of apparently satisfactory numbers was
achieved". Even after these modification, some some statistical
biases remained. The final step in producing the table of "random
digits" was to transform the table by adding pairs of digits modulo
10. This was done "in order to improve the distribution of the
digits". There were 20,000 punched cards with 50 digits per
card; each digit on a given card was added modulo 10 to the
corresponding digit of the preceding card to yield a rerandomized
digit. It is this transformed table which is published..."
This is an interesting "re-randomization" technique, since it
represents something like a convolution of the data sequence. In
other words, if the string of digits is in an array D[i] of length
1 million, the process consisted of applying the transformation
D'[i] = (D[i] + D[i-50]) mod 10
Presumably for completeness we would stipulate that the digits "wrap
around", e.g., D'[1] would equal the sum of D[1] and D[999951].
Iterations of this transformation doesn't seem to degenerate into
an orderly sequence, given a sufficiently disordered initial sequence.
In any case, results for the Rand sequence are also plotted on the
figure above, labeled as "synthesized". This sequence behaves very
differently than the digits of pi or e. It starts out quite high,
meaning that there is a scarcity of complete permutation sequences.
Eventually it settles down in the vicinity of the theoretical value,
but it seem to converge on a slightly higher value. Is there a
systematic bias in the Rand data, or does it simply require far more
digits to establish the asymptotic density of complete permutation
sequences?
To study this further, I acquired the first two million decimal digits
of the square root of 2, as computed by Nemiroff & Bonnell. The rate
of occurrence of complete permutation strings is shown in the figure
below.
 This seems to show a systematic upward bias, i.e., a scarcity of
complete permutation strings relative to the expected frequency based
on the assumption of normality. I also acquired the first million
decimal digits of the square root of 7, and of Euler's constant
gamma = 0.577... The behaviors of n/p(n) for the digits of these
two numbers are shown below.
This seems to show a systematic upward bias, i.e., a scarcity of
complete permutation strings relative to the expected frequency based
on the assumption of normality. I also acquired the first million
decimal digits of the square root of 7, and of Euler's constant
gamma = 0.577... The behaviors of n/p(n) for the digits of these
two numbers are shown below.

 The digits of the square root of 7 seem to converge fairly well on the
predicted frequency, but the digits of gamma seem to be consistently
richer in complete permutations, i.e., n/p(n) is low, at least out to
one million digits.
It may be worth noting that of all these numbers, the digits of pi
are the most thoroughly checked and verified, and those are the digits
that converge most satisfactorily to the theoretical value. For the
digits of the other constants (e, gamma, sqrt(2), sqrt(7)), Nemiroff
& Bonnell are careful to point out that they do NOT guarantee their
accuracy, and they invite other people to check them.
For another check, I acquired the first five million decimal digits
of the square root of 5 as computed by Dawson Merrill. He has actually
computed 10 million digits, but says only the first five million have
been checked, and he is confident of their correctness. The average
interval between complete permutation strings, plotted below, seems to
converge fairly well on the predicted theoretical value.
The digits of the square root of 7 seem to converge fairly well on the
predicted frequency, but the digits of gamma seem to be consistently
richer in complete permutations, i.e., n/p(n) is low, at least out to
one million digits.
It may be worth noting that of all these numbers, the digits of pi
are the most thoroughly checked and verified, and those are the digits
that converge most satisfactorily to the theoretical value. For the
digits of the other constants (e, gamma, sqrt(2), sqrt(7)), Nemiroff
& Bonnell are careful to point out that they do NOT guarantee their
accuracy, and they invite other people to check them.
For another check, I acquired the first five million decimal digits
of the square root of 5 as computed by Dawson Merrill. He has actually
computed 10 million digits, but says only the first five million have
been checked, and he is confident of their correctness. The average
interval between complete permutation strings, plotted below, seems to
converge fairly well on the predicted theoretical value.
 In any case, this raises the question of how many digits would need
to be checked in order to reasonably expect the overall frequency of
complete permutation strings to be within, say, 1% of the theoretical
asymptotic value. Also, does the speed of convergence for the digits
of a particular number have any significance. In particular, is it
significant that the decimal digits of pi evidently converge on the
asymptotic value much sooner than the digits of other irrational
numbers?
One possible way of trying to answer these questions would be to
treat the occurrence of Complete Permutation Strings (CPSs) as a
Poisson process. Of course, since the digits of overlapping strings
are not independent, this isn't exactly correct, because a Poisson
model assumes a memoryless process, i.e., it assumes that the
expected distance to the next occurrence is independent of any
prior occurrences. With CPSs this is not the case, because the
string immediately following a CPS has a probability of about 1/10
of also being a CPS (since the new digit simply needs to equal the
digit being discarded). This is roughly born out in the case of
the digits of e, because of the 778 CPSs there are 67 cases of
consecutive CPSs. There are also 6 cases of two CPSs at a distance
of 2 digits. On the other hand, it's also true that non-CPSs are
disproportionately likely to have non-CPS neighbors, because pairs
of duplicate digits are likely to be contained in the overlap of
neighboring strings.
Nevertheless, we can use the Poisson model to give a rough estimate
of the probability that the observed frequency over a given interval
differs from the asymptotic frequency by various amounts. As
discussed in Poisson Processes and Queues, the probability of
exactly k occurrences of an (exponentially distributed) event with
rate L in time (or number of trials) T is
k
(LT) -LT
P(k) = ------ e
k!
For large k we can use Stirling's formula for k! to write this in
the more easily computed form
_ _
| (k-LT)/k | k
1 | LT e |
P(k) = ------------ | ------------- |
sqrt(2k pi) |_ k _|
We examined the first T = 2,000,000 strings in the decimal expansion
of e, and found k = 778 complete permutation strings. The theoretical
rate is L = 1/2755.73, so the expected number of CPSs in this range
is LT = 725.76. The probability of finding exactly k complete strings
in the first 2 million decimal digits is shown below for k ranging
from 600 to 900.
In any case, this raises the question of how many digits would need
to be checked in order to reasonably expect the overall frequency of
complete permutation strings to be within, say, 1% of the theoretical
asymptotic value. Also, does the speed of convergence for the digits
of a particular number have any significance. In particular, is it
significant that the decimal digits of pi evidently converge on the
asymptotic value much sooner than the digits of other irrational
numbers?
One possible way of trying to answer these questions would be to
treat the occurrence of Complete Permutation Strings (CPSs) as a
Poisson process. Of course, since the digits of overlapping strings
are not independent, this isn't exactly correct, because a Poisson
model assumes a memoryless process, i.e., it assumes that the
expected distance to the next occurrence is independent of any
prior occurrences. With CPSs this is not the case, because the
string immediately following a CPS has a probability of about 1/10
of also being a CPS (since the new digit simply needs to equal the
digit being discarded). This is roughly born out in the case of
the digits of e, because of the 778 CPSs there are 67 cases of
consecutive CPSs. There are also 6 cases of two CPSs at a distance
of 2 digits. On the other hand, it's also true that non-CPSs are
disproportionately likely to have non-CPS neighbors, because pairs
of duplicate digits are likely to be contained in the overlap of
neighboring strings.
Nevertheless, we can use the Poisson model to give a rough estimate
of the probability that the observed frequency over a given interval
differs from the asymptotic frequency by various amounts. As
discussed in Poisson Processes and Queues, the probability of
exactly k occurrences of an (exponentially distributed) event with
rate L in time (or number of trials) T is
k
(LT) -LT
P(k) = ------ e
k!
For large k we can use Stirling's formula for k! to write this in
the more easily computed form
_ _
| (k-LT)/k | k
1 | LT e |
P(k) = ------------ | ------------- |
sqrt(2k pi) |_ k _|
We examined the first T = 2,000,000 strings in the decimal expansion
of e, and found k = 778 complete permutation strings. The theoretical
rate is L = 1/2755.73, so the expected number of CPSs in this range
is LT = 725.76. The probability of finding exactly k complete strings
in the first 2 million decimal digits is shown below for k ranging
from 600 to 900.
 We've also marked on this figure the value 778, which is the number
of CPSs found in the first 2,000,000 decimal digits of e. The
probability that k would be equal to or greater than 778 is only
about 2.8% based on this Poisson model.
A better method of evaluation would be to examine the digits in
disjoint blocks of 10, because these blocks would (presumably) be
statistically independent. On this basis our 2 million digits of e
represent only 200,000 independent samples, among which we would
expect to find 72.57 complete permutation strings. Now, we can
split up the digits in essentially 10 different ways, depending on
how we choose to frame the blocks. This amounts to partitioning
the 778 CPSs according to the least significant digit of their
index. Doing this, we find the following results
index CPSs
----- ------
0 87
1 71
2 80
3 74
4 82
5 76
6 81
7 68
8 85
9 74
On this basis the Poisson model is actually valid, so we can plot
these results on top of the predicted distribution as shown below.
We've also marked on this figure the value 778, which is the number
of CPSs found in the first 2,000,000 decimal digits of e. The
probability that k would be equal to or greater than 778 is only
about 2.8% based on this Poisson model.
A better method of evaluation would be to examine the digits in
disjoint blocks of 10, because these blocks would (presumably) be
statistically independent. On this basis our 2 million digits of e
represent only 200,000 independent samples, among which we would
expect to find 72.57 complete permutation strings. Now, we can
split up the digits in essentially 10 different ways, depending on
how we choose to frame the blocks. This amounts to partitioning
the 778 CPSs according to the least significant digit of their
index. Doing this, we find the following results
index CPSs
----- ------
0 87
1 71
2 80
3 74
4 82
5 76
6 81
7 68
8 85
9 74
On this basis the Poisson model is actually valid, so we can plot
these results on top of the predicted distribution as shown below.
 The average of our ten "samples" is 77.8 (although these samples are
not independent), and we can compute that the probability of this
being 78 or higher is about 27.8%. Hence it is not terribly improbable
that we would find this deviation from the expected number of CPSs
over this number of digits. It would evidently be necessary to
examine about 20 million digits to give a valid basis for drawing
a conclusion about the actual density of CPSs in the decimal digits
of e.
It's interesting that the block indices seem to bifurcate into the
odds and the evens. In fact, if we just focused on the odd blocks,
we find a mean of 72.6 CPSs per 200,000 samples, in excellent
agreement with the expected number (72.57). In contrast, the even-
indexed blocks have an average of 83 CPSs per 200,000 samples. The
probability of finding 83 or more CPSs in this range is only 12.3%.
The average of our ten "samples" is 77.8 (although these samples are
not independent), and we can compute that the probability of this
being 78 or higher is about 27.8%. Hence it is not terribly improbable
that we would find this deviation from the expected number of CPSs
over this number of digits. It would evidently be necessary to
examine about 20 million digits to give a valid basis for drawing
a conclusion about the actual density of CPSs in the decimal digits
of e.
It's interesting that the block indices seem to bifurcate into the
odds and the evens. In fact, if we just focused on the odd blocks,
we find a mean of 72.6 CPSs per 200,000 samples, in excellent
agreement with the expected number (72.57). In contrast, the even-
indexed blocks have an average of 83 CPSs per 200,000 samples. The
probability of finding 83 or more CPSs in this range is only 12.3%.