In quantum theory the condition of a physical system is represented by a state vector, which encodes the probabilities of each possible result of whatever measurements we may perform on the system. Since the probabilities are usually neither 0 nor 1, it follows that for a given system with a specific state vector, the results of measurements generally are not uniquely determined. Instead, there is a set (or range) of possible results, each with a specific probability. Furthermore, according to the conventional interpretation of quantum mechanics (the "Copenhagen Interpretation" advocated by Niels Bohr, et al), the state vector is the most complete possible description of the system, which implies that nature is fundamentally probabilistic (i.e., non-deterministic).
However, it's natural to question whether this interpretation is correct, or whether there might be some more complete description of a system, such that a fully specified system would respond deterministically to any measurement we might perform. Such proposals are called 'hidden variable' theories.
In his assessment of hidden variable theories in 1932, John von Neumann pointed out a set of five assumptions which, if we accept them, imply that no hidden variable theory can possibly give deterministic results for all measurements. The first four of these assumptions are fairly unobjectionable, but the fifth seems much more arbitrary, and has been the subject of much discussion. (The parallel with Euclid's postulates, including the controversial fifth postulate discussed in Chapter 3.1, is striking.)
To understand von Neumann's fifth postulate, notice that although the conventional interpretation does not uniquely determine the outcome of a particular measurement for a given state, it does predict a unique 'expected value' for that measurement. Let's say a measurement of X on a system with a state vector f has an expected value denoted by <X;f >, computed by simply adding up all the possible results multiplied by their respective probabilities. Not surprisingly, the expected values of observables are additive, in the sense that
![]()
![]()
![]() <X+Y;f > = <X;f > + <Y;f >
<X+Y;f > = <X;f > + <Y;f > ![]()
![]()
![]() (1)
(1)
In practice we can't generally perform a measurement of X+Y without disturbing the measurements of X and Y, so we can't measure all three observables on the same system. However, if we prepare a set of systems, all with the same initial state vector f , and perform measurements of X+Y on some of them, and measurements of X or Y on the others, then the averages of the measured values of X, Y, and X+Y (over sufficiently many systems) will be related in accord with (1).
Remember that according to the conventional interpretation the state vector f is the most complete possible description of the system. On the other hand, in a hidden variable theory the premise is that there are additional variables, and if we specify both the state vector f AND the "hidden vector" H, the result of measuring X on the system is uniquely determined. In other words, if we let <X;f ,H> denote the expected value of a measurement of X on a system in the state (f ,H), then the claim of the hidden variable theorist is that the variance of individual measured values around this expected value is zero.
Now we come to von Neumann's controversial fifth postulate. He assumed that, for any hidden variable theory, just as in the conventional interpretation, the averages of X+Y, X and Y evaluated over a set of identical systems are additive. (Compare this with Galileo's assumption of simple additivity for the composition of incommensurate speeds.) Symbolically, this is expressed as
![]()
![]() <X+Y;f ,H> = <X;f ,H> + <Y;f ,H>
<X+Y;f ,H> = <X;f ,H> + <Y;f ,H>![]()
![]() (2)
(2)
for any two observables X and Y. On this basis he proved that the variance ("dispersion") of at least one observable's measurements must be greater than zero. (Technically, he showed that there must be an observable X such that <X2> is not equal to <X>2.) Thus, no hidden variable theory can uniquely determine the results of all possible measurements, and we are compelled to accept that nature is fundamentally non-deterministic.
However, this is all based on (2), the assumption of additivity for the expectations of identically prepared systems, so it's important to understand exactly what this assumption means. Clearly the words "identically prepared" mean something different under the conventional interpretation than they do in the context of a hidden variable theory. Conventionally, two systems are said to be identically prepared if they have the same state vector (f ), but in a hidden variable theory two states with the same state vector are not necessarily "identical", because they may have different hidden vectors (H).
Of course, a successful hidden variable theory must satisfy (1) (which has been experimentally verified), but must it necessarily satisfy (2)? Relation (1) implies that the averages of <X;f ,H>, etc, evaluated over all applicable hidden vectors H, leads to (1), but does it necessarily follow that (2) is satisfied for every (or even for ANY) specific value of H? To give a simple illustration, consider the following trivial set of data:
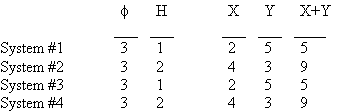
The averages over these four "conventionally indistinguishable" systems are <X;3> = 3, <Y;3> = 4, and <X+Y;3> = 7, so relation (1) holds. However, if we examine the "identically prepared" systems taking into account the hidden components of the state, we really have two different states (those with H=1 and those with H=2), and we find that the results are not additive (but they are deterministic) in these fully-defined states. Thus, equation (1) clearly doesn't imply equation (2). (If it did, von Neumann could have said so, rather than taking it as an axiom.)
Of course, if our hidden variable theory is always going to satisfy (1), we must have some constraints on the values of H that arise among "conventionally indistinguishable" systems. For example, in the above table if we happened to get a sequence of systems all in the same condition as System #1 we would always get the results X=2, Y=5, X+Y=5, which would violate (1). So, if (2) doesn't hold, then at the very least we need our theory to ensure a distribution of the hidden variables H that will make the average results over a set of "conventionally indistinguishable" systems satisfy relation (1). (In the simple illustration above, we would just need to ensure that the hidden variables are equally distributed between H=1 and H=2.)
In Bohm's 1952 theory the hidden variables consist of precise initial positions for the particles in the system - more precise than the uncertainty relations would typically allow us to determine - and the distribution of those variables within the uncertainty limits is governed as a function of the conventional state vector, f . It's also worth noting that, in order to make the theory work, it was necessary for f to be related to the values of H for separate particles instantaneously in an explicitly non-local way. Thus, Bohm's theory is a counter-example to von Neumann's theorem, but not to Bell's.
Incidentally, it may be worth noting that if a hidden variable theory is valid, and the variance of all measurements around their expectations are zero, then the terms of (2) are not only the expectations, they are the unique results of measurements for a given f and H. This implies that they are eigenvalues, of the respective operators, whereas the expectations for those operators are generally not equal to any of the eigenvalues. Thus, as Bell remarked, "[von Neumann's] 'very general and plausible postulate' is absurd".
Still, Gleason showed that we can carry through von Neumann's proof even on the weaker assumption that (2) applies to commuting variables. This weakened assumption has the advantage of not being self-evidently false. However, careful examination of Gleason's proof reveals that the non-zero variances again arise only because of the existence of non-commuting observables, but this time in a "contextual" sense that may not be obvious at first glance.
To illustrate, consider three observables X,Y,Z. If X and Y commute and X and Z commute, it doesn't follow that Y and Z commute. We may be able to measure X and Y using one setup, and X and Z using another, but measuring the value of X and Y simultaneously will disturb the value of Z. Gleason's proof leads to non-zero variances precisely for measurements in such non-commuting contexts. It's not hard to understand this, because in a sense the entire non-classical content of quantum mechanics is the fact that some observables do not commute. Thus it's inevitable that any "proof" of the inherent non-classicality of quantum mechanics must at some point invoke non-commuting measurements, but it's precisely at that point where linear additivity can only be empirically verified on an average basis, not a specific basis. This, in turn, leaves the door open for hidden variables to govern the individual results.
Notice that in a "contextual" theory the result of an experiment is understood to depend not only on the deterministic state of the "test particles" but also on the state of the experimental apparatus used to make the measurements, and these two can influence each other. Thus, Bohm's 1952 theory escaped the no hidden variable theorems essentially by allowing the measurements to have an instantaneous effect on the hidden variables, which, of course, made the theory essentially non-local as well as non-relativistic (although Bohm and others later worked to relativize his theory).
Ironically, the importance of considering the entire experimental setup (rather than just the arbitrarily identified "test particles") was emphasized by Niels Bohr himself, and it's a fundamental feature of quantum mechanics (i.e., objects are influenced by measurements no less than measurements are influenced by objects). As Bell says, even Gleason's relatively robust line of reasoning overlooks this basic insight. Of course, it can be argued that contextual theories are somewhat contrived and not entirely compatible with the spirit of hidden variable explanations, but, if nothing else, they serve to illustrate how difficult it is to categorically rule out "all possible" hidden variable theories based simply on the structure of the quantum mechanical state space.