8.4 Refractions on Relativity

We saw in Section 3.5 that Fermat's Principle of least time predicts that paths of light rays passing through a plane boundary between regions of constant refractive index, but to more fully appreciate this principle it's useful to develop the equations of motion for light rays in a medium with arbitrarily varying refractive index. First, notice that Snell's law enables us to determine the paths of optical rays passing though a discrete boundary between regions of constant refractive index, but doesn't explicitly tell us the path of light in a medium of continuously varying refractivity. To determine this, we can refer to Fresnel's equations, which give the intensities of the reflected and transmitted

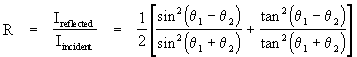
Consequently, the fraction of incident energy that is transmitted is 1 - R. However, this formula assumes the thickness of the boundaries between regions of constant refractive index is small in comparison with the wavelength of the light, whereas in many real circumstances the density of the medium does not change abruptly at well-defined boundaries, but varies continuously as a function of position. Therefore, we would like a means of tracing rays of light as they pass through a medium with a continuously varying index of refraction.

Notice that if we approximate a continuously changing index of refraction by a sequence of thin uniform plates, as we add more plates the ratio of n₂/n₁ from one region to the next approaches 1, and so according to Snell's Law the value of q ₂ approaches the value of q ₁. From Fresnel's equations we see that in this case the fraction of incident energy that is reflected goes to zero, and we find that a light ray with a given trajectory proceeds in just one direction through the continuous medium (provided the gradient of the scalar field n(x,y) is never too great relative to the wavelength of the light). So, it should be possible to predict the unique path of transmission of a light ray in a medium with continuously varying index of refraction.

Perhaps the most direct approach is via the usual calculus of variations. (For convenience we'll just work in 2 dimensions, but all the formulas can immediately be generalized to three dimensions.) We know that the index of refraction n at a point (x,y) equals c/v, where v is the velocity of light at that point. Thus, if we parameterize the path by the equations x = x(u) and y = y(u), the "optical path length" from point A to point B (i.e., the time taken by a light beam to traverse the path) is given by the integral

where dots signify derivatives with respect to the parameter u. To make this integral an extremum, let f denote the integrand function

Then the Euler equations (introduced in Section 5.4) are

which gives

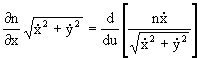
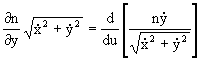
Now, if we define our parameter u as the spatial path length s, then we have , and so the above equations reduce to

(1a)

(1b)

These are the "equations of motion" for a photon in a heterogeneous medium, as they are usually formulated, in terms of the spatial path parameter s. However, another approach to this problem is to define a temporal metric on the space, i.e., a metric the represents the time taken by a light beam to travel from one point to another. This temporal approach has remarkable formal similarities to Einstein's metrical theory of gravity.

According to Fermat's Principle, the path taken by a ray of light from one point to another is such that the time is minimal (for slight perturbations of the path). Therefore, if we define a metric in the x,y space such that the metrical "distance" between any two infinitesimally close points is proportional to the time required by a photon to travel from one point to the other, then the paths of photons in this space will correspond to the geodesics.

Since the refractive index n is a smooth continuous function of x and y, it can be regarded as constant in a sufficiently small region surrounding any particular point (x,y). The incremental spatial distance from this point to the nearby point (x+dx, y+dy) is given by ds² = dx² + dy², and the incremental time dt for a photon to travel the incremental distance ds is simply ds/v where v = c/n. Therefore, we have dt = (n/c)ds, and so our metrical line element for this space is

(2)

If, instead of x and y, we name our two spatial coordinates x¹ and x² (where these superscripts denote indices, not exponents) we can express equation (2) in tensor form as

(dt)² = g_uv dx^u dx^v (3)

where g_uv is the covariant metric tensor

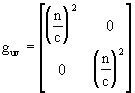
(4)

Note that in equation (3) we have invoked the usual summation convention. The contravariant form of the metric tensor, denoted by g^uv, is the matrix inverse of (4).

According to Fermat's Principle, the path of a light ray must be a geodesic path based on this metric. As discussed in Section 5.4, the equations of a geodesic path are

(5)

Based on the metric of our 2D optical space we have the eight Christoffel symbols

Inserting these into (5) gives the equations for geodesic paths, which define the paths of light rays in this region. Reverting back to our original notation of x,y for our spatial coordinates, the differential equations for ray paths in this medium of continuously varying refractive index are

(6a)

(6b)

where n_x and n_y denote partials derivatives of n with respect to x and y respectively. These are the equations of motion for light based on the temporal metric approach.

To show that these equations, based on the temporal path parameter t , are equivalent to equations (1a) and (1b) based on the spatial path parameter s, notice that s and t are linked by the relation ds/dt = c/n where c is the velocity of light. Multiplying both inside and outside the right hand side expression of (1a) by the unity of (n/c)(ds/dt ) we get

Expanding the derivative on the right side gives

Since n is a function of x and y, we can express the derivative dn/dt using the total derivative

Substituting this into the previous equation and factoring gives

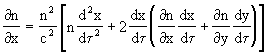
Recalling that c/n = ds/dt , we can multiply both sides of this equation by (ds/dt )² to give

Since s is the spatial path length, we have (ds)² = (dx)² + (dy)², so we can substitute for ds on the left hand side and rearrange terms to give the result

which is the same as the geodesic equation (6a). A similar derivation shows that (1b) is equivalent to the geodesic equation (6b), so the two sets of equations of motion for light rays are identical.

With these equations we can compute the locus of rays emanating from any given point in a medium with arbitrarily varying index of refraction. Of course, if the index of refraction is constant then the right hand sides of equations (6) vanish and the equations for light rays reduce to

which are simply the equations of straight lines. For a less trivial case, suppose the index of refraction in this region is a linear function of the x parameter, i.e., we have n(x) = Ax + B for some constants A and B. In this case the equations of motion reduce to

With A=5 and B=1/5 the locus of rays emanating from a point is as shown in Figure 1.

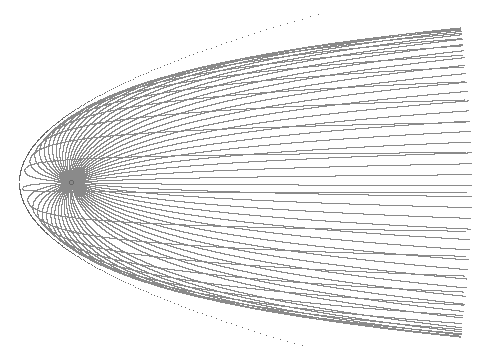Figure 1

The correctness of the rays in Figure 1 are easily verified by noting that in a medium with n varying only in the horizontal direction it follows immediately from Snell's law that the product n sin(q ) must be constant, where q is the angle which the ray makes with the horizontal axis. We can verify numerically that the rays shown in Figure 1, generated by the geodesic equations, satisfy Snell's Law throughout.

We've placed the origin of these rays at the location where n = 5. The left-most point on this family of curves emanating from that point is at the x location where n = 0. Of course, in reality we could not construct a medium with n = 0, since that represents an infinite speed of light. It is, however, possible for the index of refraction of a medium to be less than 1 for certain frequencies, such as x-rays in glass. This implies that the velocity of light exceeds c, which may seem to conflict with relativity. However, the "velocity of light" that appears in the denominator of the refractive index is actually the phase velocity, rather than the group velocity, and the latter is typically the speed of energy transfer and signal propagation. (The phenomenon of "anomalous dispersion" can actually result in a group velocity greater than c, but in all cases the signal velocity is less than or equal to c.)

Incidentally, these ray lines, in a medium with linearly varying index of refraction, are called catenary curves, which is the shape made by a heavy cable slung between two attachment points in uniform gravity. To prove this, let's first rotate the medium so that the refractive index varies vertically instead of horizontally, and let's slide the vertical axis so that n = Ay for some constant A. The general form of a catenary curve (with vertical axis of symmetry) is

for some constant m. It follows that dy/dx = sinh(x/m). Also, the incremental distance along the path is given by (ds)² = (dx)² + (dy)², so we can substitute for dy to give

(ds)² = (dx)² (1 + sinh(x/m)²) = (dx)² cosh(x/m)²

Therefore, we have ds = cosh(x/m) dx, which can be integrated to give s = sinh(x/m). Interestingly, this implies that dy/dx = s, so the slope of a catenary (with vertical axis) equals the distance along the curve from the minimum point. Also, from the relation x = m invsin(s) we have dx/ds = m / , so we can multiply this by dy/dx = s to give dy/ds = as/. Integrating this gives y as a function of s, so we have the parametric equations

x = m invsinh(s)y = m

Letting n₀ denote the index of refraction at the minimum point of the catenary (where the curve is parallel to the lines of constant refractive index), and letting A denote dn/dy, we have m = n₀/A. For other values of y we have n = Ay = n₀. We can verify that the catenary represents the path of a light ray in a medium whose index of refraction varies linearly as a function of y by inserting these expressions for x, y, and n (and their derivatives) into equations of motion (1).

The surface of revolution of one of these catenary curves about the vertical axis through the vertex of the envelope is called a catenoid. Each point inside the envelope of this family of curves is contained in exactly two curves, and the catenoid given by the shorter of these two curves is a minimal surface. It's also interesting to note that the "envelope" of rays emanating from a given point approaches a parabola whose focus is the given point. This parabola and focus are shown as a dotted line in Figure 1.

For a less trivial example, the figure below shows the rays in a medium where the index of refraction is spherically symmetrical and drops off linearly with distance from some central point, which gives ray paths that are hypocycloidal loops.

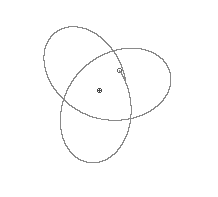Figure 2

It's also possible to arrange for the light rays to be loxodromic spirals, as shown below.

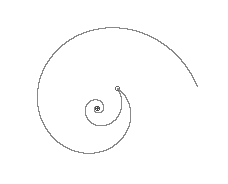Figure 3

Finally, Figure 4 shows that the rays can circulate from one point to a central point in accord with "circles of Apollonius", much like the iterations of Mobius transformations in the complex plane.

Figure 4

This occurs with n varying inversely as the square of the distance from the central point. Theoretically, the light from any point, with an initial trajectory in any direction, will eventually turn around and head toward the singularity of infinite density at the center, which the ray approaches asymptotically slowly. Thus, it might be called a "black sphere" lens that refracts all incident light toward its center. Of course, there are obvious practical difficulties with actually constructing an object like this, not least of which is the infinite density at the center, as well as the problems of reflection and dispersion.

As an aside, it's interesting to compare the light deflection predicted by the Schwarzschild solution with the deflection that would be given by a simple "refractive medium" with a scalar index of refraction defined at each point. We've seen that the "least time" metric in a plane is

where we have set c=1, and n(x,y) is the index of refraction at the point (x,y). If we write this in polar coordinates r,q , and if we assume that both n and dt/dt depend only on r, this can be written as

for some function n(r). In order to match the Schwarzschild radial speed of light dr/dt we must have n(r) = r/(r-2m), which completely determines the "refractive model" metric for light rays on the plane. The corresponding geodesic equations are

These are similar, but not identical, to the geodesic equations based on the Schwarzschild metric, as can be seen by comparing them with equations (2) in Section 6.2. The weak field deflection is almost indistinguishable. To see this, we proceed as we did with the Schwarzschild metric, integrating the second geodesic equation and determining the constant of integration from the perihelion condition at r = r₀ to give

Substituting this into the metric divided by (dt)² and solving for dr/dt gives

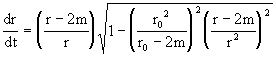
Dividing dq /dt by dr/dt gives dq /dr. Then, making the substitution r = r₀/r as before we arrive at the integral for the angular travel from the perihelion to infinity

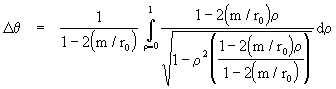
Doubling this gives the total angular travel between the incoming and outgoing asymptotes, and subtracting p from this travel gives the deflection d. Expanding the integral in powers of m/r₀, we have the result

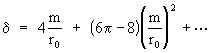
Thus the first-order deflection for this simple refraction model is the same as for the Schwarzschild solution. The solutions differ in the second order, but this difference is much too small to be measured in the weak gravitational fields found in our solar system. However, the difference would be significant near a "black hole", because the radius for lightlike circular orbits in this refractive model is 4m, as opposed to 3m for the Schwarzschild metric.

On the other hand, it's important to keep in mind that the physical significance of the usual Schwarzschild coordinates can't be taken for granted when translated into a putative model based on simple refraction. The angular coordinates are fairly unambiguous, but we have various resonable choices for the radial parameter. One common choice gives the so-called isotropic coordinates. For the radial coordinate we use r , defined with respect to the Schwarzschild coordinate r by the relation

Note that the perimeter of a circular orbit of radius r is 2pr, consistent with Euclidean geometry, whereas the perimeter of a circle of radius r is roughly 2pr(1 + m/r). In terms of this radial parameter, the Schwarzschild metric takes the form

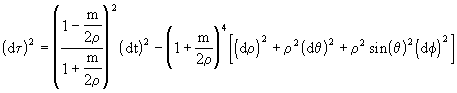
This leads to the positive-definite metric for light paths

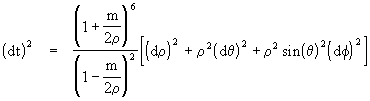
Hence if we postulate a Euclidean space with the coordinates r,q ,f centered on the mass m, and a refractive index varying with r according to the formula

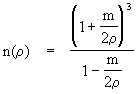
then the equations of motion for light are formally identical to those predicted by general relativity. On the other hand, when we postulate a Euclidean space with the radial parameter r we are neglecting the fact that the perimeter of a circle of radius r in this space does not have the value 2pr, so this is not an entirely self-consistent interpretation, as opposed to the usual "curvature" interpretation of general relativity. Also, it isn't self-evident that a refractive model can correctly account for the motions of time-like objects, whereas Einstein's curved-spacetime interpretation handles all these motions in a unified and self-consistent manner.