6.8 Sources in Motion
The preceding sections focused on the spherically symmetrical solution of Einstein's field equations represented by the Schwarzschild geometry, since nearly all of the experimentally observable effects of general relativity are actually just tests of Schwarzschild geometry combined with the geodesic hypothesis. (As discussed in Section 5.8, the field equations themselves, together with suitable assumptions as to the form of the mass-energy tensor, actually entail the geodesic equations of motion, but the geodesic hypothesis is fairly unobjectionable in its own right, even outside the context of the Einstein field equations.) Of course, the full field equations of general relativity admit a much wider class of solutions, notably, solutions in which metrical disturbances propagate as waves. Such waves have never (yet) been directly observed, so they don't at present constitute part of the experimentally validated body of general relativity, but there is indirect empirical confirmation of gravitational waves in the apparent energy loss of certain binary star systems, most notably the Hulse-Taylor system, which consists of a neutron star and a pulsar orbiting each other every 8 hours. Careful observations indicate that the two stars are spiraling toward each other at a rate of 2.7 parts per billion each year, precisely consistent with the prediction of general relativity for the rate at which the system should be radiating energy in the form of gravitational waves. The agreement is very impressive, and subsequent observations of other binary star systems have provided similar indirect support for the existence of gravitational waves, although in some cases it is necessary to postulate other (unseen) bodies in the system in order to yield results consistent with general relativity.
The experimental picture may change soon as a result of the LIGO project, which is an attempt to use interferometry techniques to directly detect gravitational waves. Two separate facilities are being prepared in the states of Louisiana and Washington, and their readings will be combined to achieve a very large baseline. The facility in Washington state is over a mile long. If this effort is successful in detecting gravitational waves, it will be a stupendous event, possibly opening up a new "channel" for observing the universe. Of course, it's also possible that LIGO may yield inconclusive results, i.e., no waves may be definitely detected, but it may be unclear whether the test has been adequate to detect them even if they were present.
If, on the other hand, the LIGO effort were to surprise us with an unambiguously null result (like the Michelson-Morley experiments), ruling out the presence of gravitational waves in a range where theory says they ought to be detectable, it could have serious implications for the field equations and/or the quadrupole solution. Oddly enough, Einstein became convinced for a short time in 1937 that gravity waves were impossible, but soon changed his mind again. As recently as the General Relativity conference in 1980 there were disputes as to the validity of the quadrupole solution. Part of the reason that people such as Einstein have occasionally doubted the reality of the wave solutions is that all gravitational waves imply a singularity (as does the Schwarzschild solution), albeit "merely" a coordinate singularity. Also, the phenomena of gravitational waves must be inherently non-linear, because it consists of gravity "acting on itself", and we know that gravity itself doesn't show up in the source terms of the field equations, but only in the non-linearity of the left-hand side of the field equations. The inherent non-linearity of gravitational waves makes them difficult to treat mathematically, because the classical wave solutions are based on linearized models, so it isn't easy to be sure the resulting "solutions" actually represent realistic solutions of the full non-linear field equations. Furthermore, there are no known physical situations that would produce any of the simple linearized plane wave situations that are usually discussed. For example, it is known that there are no plane wave solutions to the non-linear field equations. There are cylindrical solutions, but unfortunately no plausible sources for infinite cylindrical solutions are known, so the physical significance of these solutions is unclear.
It might seem as though there ought to be spherically symmetrical "pulsating" solutions that radiate gravitational waves, but this is not the case, as is clear from Birkhoff's proof that the Schwarzschild solution is the unique (up to transformation of coordinates) spherically symmetrical solution of the field equations, even without the "static" assumption. This is because, unlike the case of electromagnetism, the gravitational field is also the metric by which the field is measured, so coordinate transformations inherently represent more degrees of freedom than in Maxwell's equations, which have just a single "gage". As a result, there is no physically meaningful "dipole" source for gravitational waves in general relativity. The lowest-order solutions are necessarily given by quadrupole configurations.
Needless to say, another major complication in the consideration of gravitational waves is the idea of "gravitons" arising from attempts to quantize the gravitational field by analogy with the quantization of the electromagnetic field. This moves us into a realm where the classical notions of a continuous spacetime manifold may not be sustainable. A great deal of effort has been put into understanding how the relativistic theory of gravity can be reconciled with quantum theory, but no satisfactory synthesis has emerged. Regardless of future developments, it seems safe to say that the results associated with the large-scale Schwarzschild metric and geodesic hypothesis would not be threatened by quantization of the field equations. Nevertheless, this shows how important the subject of gravitational waves is for any attempt to integrate the results of general relativity into quantum mechanics (or vice versa, as Einstein might have hoped). This is one reason LIGO's results are so eagerly awaited.
Closely related to the subject of gravitational waves is the question of how rapidly the "ordinary" effects of gravity "propagate". It's not too surprising that early investigations of the gravitational field led to the notion of instantaneous action at a distance, because it is an empirical fact that the gravitational acceleration of a small body orbiting at a distance r from a gravitating source points, at each instant, very precisely toward the position of the source at that instant, not (as we might naively expect) toward the location of the source at a time r/c earlier. (When we refer to "instants" in this section, we mean with respect to the inertial rest coordinates of the center of mass of the orbital system.) The gain a clear understanding of the reason for the absence of gravitational "aberration" in these circumstances, it's useful to recall some fundamentals of the phase relations between dynamically coupled variables. One of the simplest representations of dynamic coupling between two variables x and y is the "lead-lag" transfer function, which is based on the ordinary first-order differential equation
![]()
where a0, a1, b0, and b1 are constants. This coupling is symmetrical, so there is no implicit directionality, i.e., we aren't required to regard either x or y as the independent variable and the other as the dependent variable. However, in most applications we are given one of these variables as a function of time, and we use the relation to infer the response of the other variable. To assess the "frequency response" of this transfer function we suppose that the x variable is given by a pure sinusoidal function x(t) = Asin(wt) for some constants A and w. Eventually the y variable will fall into an oscillating response, which we presume is also sinusoidal of the same frequency, although the amplitude and phase may be different. Thus we seek a solution of the form
y(t) = Bsin(wt - q )
for some constants B and q . If we define the "time lag" tL of the transfer function as the phase lag q divided by the angular frequency w , it follows that the time lag is given by
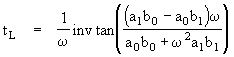
For sufficiently small angular frequencies the input function and the output response both approach simple linear "ramps", and since invtan(z) goes to z as z approaches zero, we see that the time lag goes to
![]()
The ratios a1/a0 and b1/b0 are often called, respectively, the lag and lead time constants of the transfer function, so the "time lag" of the response to a steady ramp input equals the lag time constant minus the lead time constant. Notice that it is perfectly possible for the lead time constant to be greater than the lag time constant, in which case the "time lag" of the transfer function is negative. In general, for any frequency input (not just linear ramps), the phase lag is negative if b1/b0 exceeds a1/a0. Despite the appearance, this does not imply that the transfer function is somehow reads the future, nor than the input signal is traveling backwards in time (or is instantaneous in the case of a symmetrical coupling). The reason the output appears to anticipate the input is simply that the forcing function (the right hand side of the original transfer function) contains not only the input signal x(t) but also its derivative dx/dt (assuming b1 is non-zero), whose phase is p/2 ahead. (Recall that the derivative of the sine is the cosine.) Hence a linear combination of x and its derivative yields a net forcing function with an advanced phase.
Thus the effective forcing function at any given instant does not reflect the future of x, it represents the current x and the current dx/dt. It just so happens that if the sinusoidal wave pattern continues unchanged, the value of x will subsequently progress through the phase that was "predicted" by the combination of the previous x and dx/dt signals, making it appear as though the output predicted the input. However, if the x signal abruptly changes the pattern at some instant, the change will not be foreseen by the output. Any such change will only reach the output after it has appeared at the input and worked its way through the transfer function. One way of thinking about this is to remember that the basic transfer function is directionally symmetrical, and the "output signal" y(t) could just as well be regarded as the input signal, driving the "response" of x(t) and its derivative.
We sometimes refer to "numerator dynamics" as the cause of negative time lags, because the b1 coefficient appears in the numerator of the basic dynamic relationship when represented as a transfer function with x(t) as an independent "input" signal. The ability of symmetrical dynamic relations to extrapolate periodic input oscillations so that the output has the same phase as (or may even lead) the input accounts for many interesting effects in physics. For example, in electrodynamics the electrostatic force exerted on a uniformly moving test particle by a "stationary" charge always points directly toward the source, because the field is spherically symmetrical about the source. However, since the test particle is moving uniformly we can also regard it as "stationary", in which case the source charge is moving uniformly. Nevertheless, the force exerted on the test particle always points directly toward the source at the present instant. This may seem surprising at first, because we know changes in the field propagate at the speed of light, rather than instantaneously. How does the test particle "know" where the source is at the present instant, if it can only be influenced by the source at some finite time in the past, allowing for the finite speed of propagation of the field? The answer, again, is numerator dynamics. The electromagnetic force function depends not only on the source's relative position, but also on the derivative of the position (i.e., the velocity). The net effect is to cancel out any phase shift, but of course this applies only as long as the source and the test particle continue to move uniformly. If either of them is accelerated, the "knowledge" of this propagates from one to the other at the speed of light.
An even more impressive example of the phase-lag cancellation effects of numerator dynamics involves the "force of gravity" on a massive test particle orbiting a much more massive source of gravity, such as the Earth orbiting the Sun. In the case of Einstein's gravitational field equations the "numerator dynamics" cancel out not only the first-order phase effects (like the uniform velocity effect in electromagnetism) but also the second-order phase effects, so that the "force of gravity" on an orbiting points directly at the gravitating source at the present instant, even though the source (e.g., the Sun) is actually undergoing non-uniform motion. In the two-body problem, both objects actually orbit around the common center of mass, so the Sun (for example) actually proceeds in a circle, but the "force of gravity" exerted on the Earth effectively anticipates this motion.
The reason the phase cancellation extends one order higher for gravity than for electromagnetism is the same reason that Maxwell's equations predict dipole waves, whereas Einstein's equations only support quadrupole (or higher) waves. Waves will necessarily appear in the same order at which phase cancellation no longer applies. For electrically charged particles we can generate waves by any kind of acceleration, but this is because electromagnetism exists within the spacetime metric provided by the field equations. In contrast, we can't produce gravitational waves by the simplest kind of "acceleration" of a mass, because there is no background reference to unambiguously define dipole acceleration. The Einstein field equations have an extra degree of freedom (so to speak) that prevents simple dipole acceleration from having any "traction". It is necessary to apply quadrupole acceleration, so that the two dipoles can act on each other to yield a propagating effect.
In view of this, we expect that a two-body system such as the Sun and the Earth, which essentially produces no gravitational radiation (according to general relativity) should have numerator dynamic effects in the gravitational field that give nearly perfect phase-lag cancellation, and therefore the Earth's gravitational acceleration should always point directly toward the Sun's position at the present instant, rather than (say) the Sun's position eight minutes ago. Of course, if something outside this two-body system (such as a passing star) were to upset the Sun's pattern of motion, the effect of such a disturbance would propagate at the speed of light. The important point to realize is that the fact that the Earth's gravitational acceleration always points directly at the Sun's present position does not imply that the "force of gravity" is transmitted instantaneously. It merely implies that there are velocity and acceleration terms in the transfer function (i.e., numerator dynamics) that effectively cancel out the phase lag in a simple periodic pattern of motion.