6.2 Anomalous Precessions

The Earth's equatorial plane maintains a nearly constant absolute orientation in space throughout the year due to the gyroscopic effect of spinning about its axis. Similarly the plane of the Earth's orbit around the Sun remains essentially constant. These two planes are tilted by 23.5 degrees with respect to each other, so they intersect along a single line whose direction remains constant, assuming the planes themselves maintain fixed attitudes. At the Spring and Autumn equinoxes the Sun is located precisely on this fixed line in opposite directions from the Earth. Since this line is a highly stable directional reference, it has been used by astronomers since ancient times to specify the locations of celestial objects. (Of course, when we refer to "the location of the Sun" we are speaking somewhat loosely. With the increased precision of observations made possible by the invention of the telescope, it is strictly necessary to account for the Sun's motion about the center of mass of the solar system. It is this center of mass of the Sun and planets, rather than just of the Sun, that is taken as the central inertial reference point for the most precise astronomical measurements and calculations.) By convention, the longitude of celestial objects is referenced from the direction of this line pointing to the Spring equinox, and this is called the "right ascension" of the object. In addition, the "declination" specifies the latitude, i.e., the angular position North or South of the Earth's equatorial plane.

This system of specifying positions is quite stable, but not perfect. Around 150 BC the Greek astronomer Hipparchus carefully compared his own observations of certain stars with observations of the same stars recorded by Timocharis 169 years earlier (and with some even earlier measurements from the Babylonians), and noted a slight but systematic difference in the longitudes. Of course, these were all referenced to the supposedly fixed direction of the line of intersection between the Earth's rotational and orbital planes, but Hipparchus was led to the conclusion that this direction is not perfectly stationary, i.e., that the direction of the Sun at the equinoxes is not constant with respect to the fixed stars, but precesses by about 0.0127 degrees each year. This is a remarkably good estimate, considering the limited quality of the observations that were available to Hipparchus. The accepted modern value for the precession of the equinoxes is 0.01396 degrees per year, which implies that the line of the equinoxes actually rotates completely around 360 degrees over a period of about 26,000 years. Interpreting this as a gradual change in the orientation of the Earth's axis of rotation, the precession of the equinoxes is the third of what Copernicus called the "threefold movement of the Earth", the first two being a rotation about its axis once per day, and a revolution about the Sun once per year. Awareness of this third motion is arguably a distinguishing feature of human culture, since it can only be discerned on the basis of information spanning multiple generations.

The reason for mentioning this, aside from expressing admiration for human ingenuity, is that when we observe the axis of the elliptical orbit of a planet such as Mercury (for example) over a long period of time, referenced to our equinox line, we must expect to find an apparent precession of about 0.01396 degrees per year, which equals 5025 arc seconds per century, assuming Mercury's orbital axis is actually stationary. However, astronomers have actually observed a precession rate of 5600 arc seconds per century for the axis of Mercury's orbit, so evidently the axis is not truly stationary. This might seem like a problem for Newtonian gravity, until we remember that Newton predicted stable elliptical orbits only for the idealized two-body case. When analyzing the actual orbit of Mercury we must also take into account the gravitational pull of the other planets, especially Venus and Earth (because of their proximity) and Jupiter (because of its size). It isn't simple to work out these effects, and unfortunately there is no simple analytical solution to the n-body problem in Newtonian mechanics, but using the calculational techniques developed by Lagrange, Laplace, and others, it is possible to determine that the effects of all the other planets should contribute an additional 532 arc seconds per century to the precession of Mercury's orbit. Combined with the precession of our equinox reference line, this accounts for 5557 arc seconds per century, which is close to the observed value of 5600, but still short by 43 arc seconds per century. The astronomers assure us that their observations can't be off by more than a fraction of an arc second, so there seems to be a definite problem here.

A similar problem had appeared in the 1840's when the newly discovered planet Uranus began to deviate noticeably from the precise course that Newtonian theory prescribed. On that occasion, the astronomer Le Verrier and the mathematician Adams had (independently) inferred the existence of a previously unknown planet beyond the orbit of Uranus, and even gave instructions where it could be found. Sure enough, when that indicated region of the sky was searched by Johann Galle at the Berlin Observatory, the planet that came to be called Neptune was discovered in 1846, astonishingly close to the predicted location. This was a tremendous triumph for Le Verrier, and surely gave him confidence that all apparent anomalies in the planetary orbits could be explained on the basis of Newtonian theory, and could be used as an aid to the discovery of new celestial objects. He soon turned his attention to the anomalous precession of Mercury's orbit (which he estimated at 38 arc seconds per century, somewhat less than the modern value), and suggested that it must be due to some previously unknown mass near the Sun, possibly a large number of small objects, or perhaps even another planet, inside the orbit of Mercury.

At one point there were reports that a small planet orbiting very near the Sun had actually been sighted, and it was named Vulcan, after the Roman God of fire. Le Verrier became convinced that the new planet existed, but subsequent attempts to observe the hypothetical planet failed to find any sign of it. Even the original sightings were cast into doubt, since they had been made by an amateur, and other astronomers reported that they had been observing the Sun at the very same time and had seen nothing. Another popular theory to explain Mercury's anomalous precession, championed by the astronomer Simon Newcomb, was that the small particles of matter that cause the "zodiacal light" might account for Mercury's anomalous precession, but Newcomb soon realized that if there were enough matter to affect Mercury's perihelion so significantly there would also be enough to cause other effects on the orbits of the inner planets - effects which are not observed. Similar problems afflicted any theory of the planet Vulcan.

As a result of the failures to arrive at a realistic Newtonian explanation for the anomalous precession, some researchers, notably Asaph Hall and Newcomb, began to think that perhaps Newtonian theory was at fault, and that perhaps gravity isn't exactly an inverse square law. Hall noted that he could account for Mercury's precession if the law of gravity, instead of falling off as 1/r², actually falls of as 1/rⁿ where the exponent n is 2.00000016. However, most people didn't (and still don't) find that idea to be very appealing, since it conflicts with basic conservation laws, e.g., Gauss's Law, unless we also postulate a correspondingly modified metric for space (ironically enough).

More recently, efforts have been made to explain some or all of Mercury's precession by oblateness in the shape of the sun. In 1966 Dicke and Goldenberg reported that the sun's polar axis is shorter than its equatorial axes by about 50 parts per million. If true that would account for 3.4" per century, so the unexplained part would be only 39.6", significantly different from GR's prediction of 43". The Brans-Dicke theory of gravity can account for 39.6" precisely by adjusting a free parameter of the theory. However, Dicke's and Goldenberg's solar oblateness data was contradicted by a number of other heliometric measurements, all of which showed that the solar axes differ by no more than about 4 parts per million. In addition, the sun doesn't appear to rotate nearly fast enough to be as oblate as Dicke and Goldenberg thought, so their results could only be right if the interior of the sun is spinning about 25 times faster than the visible exterior, which is highly implausible.

The current consensus is that the Sun is not nearly oblate enough to upset the agreement between Mercury's observed precession and the predictions of GR. This is all the more impressive considering that, in contrast to the Brans-Dicke and other alternative theories, GR has almost no "freedom" to adjust its predictions. It is highly constrained by its own logic, so it's remarkable that it continues to survive experimental challenges.

By the way, it may be worth noting that Mercury isn't the only object in the solar system that exhibits anomalous precession. The effect is most noticeable for objects near the Sun with highly elliptical orbits, but it can be seen even in the nearly circular orbits of Venus and Earth, although the discrepancy isn't nearly so large as for Mercury. In addition, the asteroid Icarus is ideal for studying this effect, because it has an extremely elliptical orbit and periodically passes very close to the Sun. Here's a table showing the anomalous precession of four objects in the inner solar system, based on direct observations:

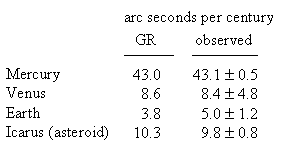
The large tolerances for Venus and Earth are mainly due to the fact that their orbits are so nearly circular, making it difficult to precisely determine the axes of their elliptical orbits.

Incidentally, Icarus periodically crosses the Earth's path, and has actually passed within a million kilometers of us - less than 3 times the distance to the Moon. It's about 1 mile in diameter, and may eventually collide with the Earth - reason enough to keep an eye on that precession.

One hope that Einstein had in mind throughout the time he was working on the general theory was that the final theory would explain the anomalous precession of Mercury. Of course, as we've seen, "explanations" of this phenomenon were never in short supply, but none of them were very compelling, all seeming to be ad hoc.

To determine the relativistic prediction for the advance of an elliptical orbit, let's work in the single plane f =0, so of course df /dt and all higher derivatives also vanish. Then the term involving f in the Schwarzschild metric drops out, leaving just

and the equations of geodesic motion, with the parameter l equal to the proper time t, are

We can immediately integrate equations (2) and (4) to give

where k and h are constants of integration, determined by the initial conditions of the orbit. We can now substitute for these derivatives into the basic Schwarzschild metric divided by (dt)² to give

Solving for (dr/dt)², we have

Differentiating this with respect to t and dividing by 2(dr/dt) gives

Letting w = dq /dt denote the proper angular speed, we have h = r^2w , and the above equation can be written as

Obviously if w = 0 this gives the "proper" analog of Newton's inverse-square law for radial gravitational acceleration. With non-zero w the term w²r corresponds to the Newtonian centripetal acceleration which, if we defined the tangential velocity v = wr, would equal the classical v²/r. This term serves to offset the inward pull of gravity, but in the relativistic version we find not w²r but w²(r-3m). For values of r much greater than 3m this difference can be neglected, but clearly if r approaches 3m we can expect to see non-classical effects, and of course if r ever becomes less than 3m we would expect completely un-classical behavior. In fact, this corresponds to the cases when an orbiting particle spirals into the center, which never happens in classical theory (see below).

Since the above equations involve powers of (1/r) it's convenient to work with the parameter u = 1/r. Differentiating u with respect to q gives du/dq = -(1/r²) dr/dq. Also, since r² = h/(dr/dt), we have dr/dt = -h (du/dq). Substituting for dr/dt and 1/r into equation (5) gives the following differential equation relating u to q

Differentiating again with respect to q and dividing by 2h² (du/dq), we arrive at

where denotes d²u/dq². Solving this quadratic for u gives

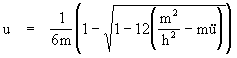
The quantity in the parentheses under the square root is typically quite small compared with 1, so we can approximate the square root by the first few terms of its expansion

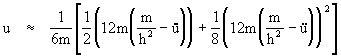
Expanding the right hand side and re-arranging terms gives

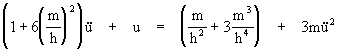
The value of in typical astronomical problems is numerically quite small (many orders of magnitude less than 1), so the quantity 3m² on the right hand side will be negligible for planetary motions. Therefore, we're left with a simple harmonic oscillator of the form where M and F are constants. For some choice of initial q the general solution of this equation can be expressed as where k is a constant of integration. Therefore, reverting back to the parameter r = 1/u, the relation between r and q is

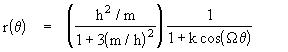where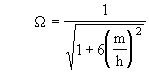

If the "frequency" W was equal to unity, this would be the polar equation of an ellipse with the pole at one focus, and the constant k would signify the eccentricity. Also, the leading factor would be the radial distance from the focus to the ellipse at an angle of p/2 from the major axis, i.e., it would represent the semilatus rectum. However, the value of W is actually slightly less than 1, which implies that q must go slightly beyond 2p in order to complete one cycle of the radial distance. Consequently, for small values of m/h the path is approximately a Keplerian ellipse, but the axis of the ellipse precesses slightly, as illustrated below.

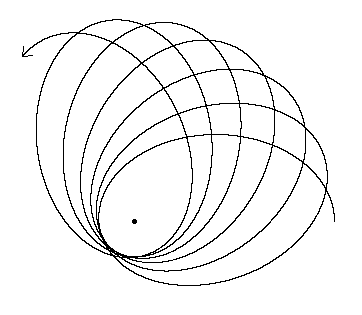
This illustration depicts a much more severe case than could exist for any planet in our solar system, because the perihelion of the orbit is only 200m where m is the gravitational radius (in geometrical units) of the central object, which means it is only 100 times the corresponding "black hole radius". Our Sun's mass is not nearly concentrated enough to permit this kind of orbit, since the Sun's gravitational radius is only m = 1.475 kilometers, whereas it's matter fills a sphere of radius 696,000 kilometers.

To determine the relativistic prediction for the orbital precession of the planetary orbits, we can expand the expression for W as follows

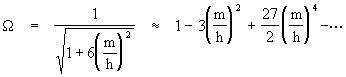
Since m/h is so small, we can take just the first-order term, and noting that one cycle of the radial function will be completed when W q = 2p , we see that q must increase by 2p/W for each radial cycle, so the precession per revolution is

We saw above that the semilatus rectum L is approximately h²/m, so the amount of precession per revolution (for slow moving objects in weak gravitational fields, such as the planets in our solar system) can be written as simply 6pm/L, where m is the gravitational radius of the central body. As noted above, the gravitational radius of our Sun is 1.475 kilometers, so based on the elements of the planetary orbits we can construct the following table of relativistic precession.

         Semimajor    Orbital  Semilatus  Precession  Revs  Precession
            Axis       Eccen    Rectum, L   per rev    per   per century
 Planet  (million km)     k    (million km)(arc sec)  century (arc sec)

  Mercury    57.9000   0.2060     55.4430   0.1034   414.9378   42.9195
  Venus     108.2000   0.0070    108.1947   0.0530   162.6016    8.6186
  Earth     149.6000   0.0170    149.5568   0.0383   100.0000    3.8345
  Mars      227.9000   0.0930    225.9289   0.0254    53.1915    1.3502
  Jupiter   778.3000   0.0480    776.5068   0.0074     8.4317    0.0623
  Saturn   1427.0000   0.0560   1422.5249   0.0040     3.3944    0.0137
  Uranus   2869.6000   0.0470   2863.2611   0.0020     1.1903    0.0024
  Neptune  4496.6000   0.0090   4496.2358   0.0013     0.6068    0.0008
  Pluto    5900.0000   0.2500   5531.2500   0.0010     0.4032    0.0004

The observed precession of 43.1 � 0.5 arc seconds per century for the planet Mercury is in close agreement with the theory. We noted in section 5.8 how Einstein proudly concluded his presentation of the vacuum field equations in his 1916 paper on general relativity by pointing out that they explained the anomalous precession of Mercury. He returned to this subject at the end of the paper, giving the precession formula and closing his masterpiece with the words

We mentioned previously that the small eccentricities of Venus and Earth make it difficult to determine their lines of apsides with precision, but modern measurement techniques (including the use of interplanetary space probes and radar ranging) and computerized analysis of the data have enabled the fitting of the entire solar system to a parameterized post-Newtonian (PPN) model that encompasses a fairly wide range of theories (including general relativity). Once the parameters of this model have been fit to all the available data for the Sun and planets, the model can then be used to compute the "best observational fit" for the precessions of the individual planets based on the PPN formalism. This gives precessions (in excess of the Newtonian predictions) of 43.1, 8.65, 3.85, and 1.36 arcseconds per century for the four inner planets respectively, in remarkable agreement with the predictions of general relativity.

If we imagine an extremely dense central object, whose mass is concentrated inside it's gravitational radius, we can achieve much greater deviations from conventional Newtonian orbits. For example, if the precession rate is roughly equal to the orbital rate, we have an orbit as shown below:

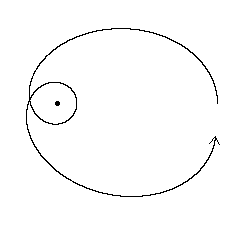
For an orbit with slightly less energy the path looks like this:

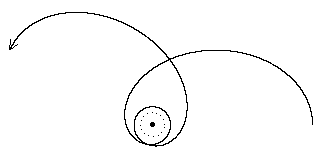
where the dotted circle signifies the "light orbit" radius r = 3m. With sufficient angular momentum it's possible to arrange for persistent timelike orbits periodically descending down to any radius greater than 3m, which is the smallest possible radius of a circular orbit (but note that a circular orbit with radius less than 6m is unstable). If a timelike geodesic ever passes inside that radius it must then spiral in to the central mass, as illustrated below.

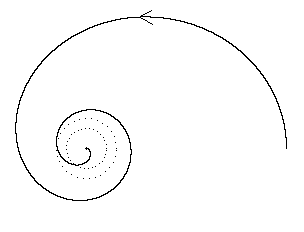
Here the outer dotted circle is at 3m, and the inner circle is at the event horizon, 2m. Once a worldline has fallen within 2m, whether geodesic or not, it's radial coordinate must (according to the Schwarzschild solution) thereafter decrease monotonically to zero.

Regarding these spiral solutions there is an ironic historical precedent. A few years before writing the Principia Newton once described in a letter to Robert Hooke the descent of an object along a spiral path to the center of a gravitating body. Several years later, after the Principia had established Newton's reputation, the two men became engaged in a bitter priority dispute over the discovery of universal gravitation, and Hooke used this letter as evidence that Newton hadn't understood gravity at that time, because the classical inverse-square law of gravity permits no such spiral solutions. Newton replied that it had simply been a "negligent stroke with his pen". Interestingly, although people sometimes credit Newton with originating the idea of photons based on his erroneous corpuscular theory of light, it's never been suggested that his "negligent spiral" was a premonition of the Schwarzschild solution of Einstein's field equations.

Incidentally, the relativistic contribution to a planet's orbital precession rate is often derived on the basis of "resonance". The general solution of an ordinary linear differential equation contains a term proportional to e^lx for each root l of the characteristic polynomial. A resonance occurs when the characteristic polynomial has a repeated root, in which case the solution has a term proportional to xe^lx, and if there is another repetition of the root it is represented by a term proportional to x²e^lx, and so on. Similarly as a means of approximating the solution of many authors introduce a "resonant" trial solution of the form c₀ + c₁cos(q) + c₂qsin(q), suggesting that the last term is to be regarded as a resonance, whose effect grows cumulatively over time because the factor q is not periodic, and therefore eventually has observable effects. However, they then go on to invoke the small-angle approximation in order to apply the trigonometric identity cos(x+y) = cos(x)cos(y) - sin(x)sin(y) to reduce the solution to the form c₀ + c₃ cos(W q). Although this yields the correct result, the interpretation of it as a resonance effect seems misleading, because the predominant cumulative effect of a resonant term proportional to qsin(q) is not an on-going precession of the ellipse, but rather an increase in the magnitude of the radial excursions, which doesn't correspond to anything in the actual relativistic behavior of orbits. This unrealistic increase in the radial excursion is what causes the perihelion and aphelion on the initial cycles to "precess" slightly, simply because the phase of the sine component is beginning to assert itself over the phase of the cosine component. In other words, the "precession" resulting from the qsin(q) term on the first cycle is really just a phase shift corresponding to an unrealistic secular increase in the radial amplitude, and does not signify a secular change in the frequency of the solution. This approach arrives at the correct approximate effect only by compounding two errors, first introducing the unrealistic "resonance" term qsin(q) as if it's secular effect was a change in frequency, and then immediately throwing away its secular effect (which is really a change in amplitude) by using the small angle approximation to produce an apparent change in the secular frequency.