4.5 Conventional Wisdom

It is a matter of empirical fact that the speed of light is invariant with respect to inertial coordinate systems, and yet the invariance of the speed of light is often said to be a matter of convention - as indeed it is. How can an empirical fact be conventional? It can't, and nothing we have said implies that it can. Our statement of empirical fact refers to the speed of light with respect to inertial coordinates, whereas our statement of convention merely makes an assertion about the "speed" of light, without specifying how this speed is to be defined. Hence the latter statement is obviously a matter of convention, because we can define systems of space and time coordinates with respect to which it is true, and other systems with respect to which it is false. Of course, our statement of empirical fact regarding the speed of light in terms of inertial coordinates would be circular if inertial coordinates were simply defined as systems with respect to which the speed of light is invariant. However, as discussed below, the class of inertial coordinate systems can be defined in purely mechanical terms, without referring to the propagation of light, so the empirical invariance of light speed with respect to this class of coordinate systems has non-trivial physical content.

The conventionalist view can be traced back to Poincare, who wrote in "The Measure of Time" in 1898

In the same paper, Poincare described the use of light rays, together with the convention that the speed of light is invariant and the same in all directions, to give an operational meaning to the concept of simultaneity. In his book "Science and Hypothesis" (1902) he summarized his view of time by saying

Poincare's views had a strong influence on the young Einstein, who avidly read "Science and Hypothesis" with his friends in the self-styled "Olympia Academy". Solovine remembered that this book "profoundly impressed us, and left us breathless for weeks on end". Indeed we find in Einstein's 1905 paper on special relativity the statement

In a later popular exposition, Einstein tried to make the meaning of this definition more clear by saying

Of course, this concept of simultaneity is also embodied in Einstein's second "principle", which asserts the invariance of light speed. Throughout the writings of Poincare, Einstein, and others, we see the invariance of the speed of light referred to as a convention, a definition, a stipulation, a free choice, an assumption, a postulate, and a principle... as well as an empirical fact. How are we to reconcile all these characterizations?

There is actually no conflict at all, because the convention (definition, stipulation, free choice, principle) that Poincare and Einstein were referring to is nothing other than the decision to use inertial coordinate systems. As Poincare said in 1898, we naturally choose our coordinate systems "in such a way that the statements of the natural laws are as simple as possible", and this almost invariably means inertial coordinates. It was the great achievement of Galileo, Descartes, Huygens, and Newton to identify the principle of inertia as the basis for resolving and coordinating physical phenomena. Unfortunately this insight is often disguised by the manner in which it is traditionally presented. The beginning physics student is typically expected to accept uncritically an intuitive notion of "uniformly moving" time and space coordinate systems, and is then told that Newton's laws of motion happen to be true with respect to those "inertial" systems. It is more meaningful to say that we define inertial coordinate systems as those systems in terms of which Newton's laws of motion are valid. This is because we naturally coordinate events and organize our perceptions in such a way as to maximize symmetry, and for the motion of material objects the most important symmetries are the isotropy of inertia, the conservation of momentum, the law of equal action and re-action, and so on. Newtonian physics is organized entirely upon the principle of inertia, and the basic underlying hypothesis is that for any object in any state of motion there exists a system of coordinates in terms of which the object is instantaneously at rest and Newton's laws of motion are valid (at least for quasi-static motions).

The empirical validity of this remarkable hypothesis accounts for all the tremendous success of Newtonian physics. As discussed in Section 1.3, the specification of a particular state of motion, combined with the requirement for Newton's laws to be quasi-statically valid, completely determines a system of coordinates (up to insignificant scale factors, rotations, etc), and such a system is called an inertial system of coordinates. Such coordinate systems can be established unambiguously by purely mechanical means (neglecting the equivalence principle and associated complications). The assumption of inertial isotropy with respect to a given state of motion suffices to establishes the loci of inertial simultaneity for that state of motion. Poincare and Einstein rightly noted the conventionality of this simultaneity definition because they were not pre-supposing the choice of inertial simultaneity. In other words, we are not required to use inertial coordinates. We simply choose, of our own free will, to use inertial coordinates - with the corresponding inertial definition of simultaneity - because this renders the statement of physical laws and the descriptions of physical phenomena as simple as possible, by taking advantage of the maximum possible symmetry.

It's important to remember that inertial coordinates are not entirely characterized by the quality of being unaccelerated, i.e., by the requirement that isolated objects move uniformly in a straight line. It's also necessary to require the unique simultaneity convention that renders mechanical inertial isotropic (the same in all spatial directions), which amounts to the stipulation of equal one-way speeds for the propagation of physically identical actions. These comments are fully applicable to the Newtonian concept of space, time, and inertial reference frames. Given two objects in relative motion we can define two systems of inertial coordinates in which the respective objects are at rest, and we can orient these coordinates so the relative motion is purely in the x direction. Let t,x and T,X denote these two systems of inertial coordinates. That such coordinates exist is the main physical hypothesis underlying Galilean physics. An auxiliary hypothesis, one that was not always clearly recognized, concerns the relationship between two such systems of inertial coordinates, given that they exist. Galileo assumed that if the coordinates x,t of an event are known, and if the two inertial coordinate systems are the rest frames of objects moving with a relative speed of v, then the coordinates of that event in terms of the other system (with suitable choice of origins) are T = t, X = x - vt. Viewed in the abstract, this is a rather peculiar and asymmetrical assumption, although it is admittedly borne out by experience - at least to the precision of measurement available to Galileo. However, we now know, empirically, that the relation between relatively moving systems of inertial coordinates is the symmetrical form T = (t - vx)/g and X = (x - vt)/g where g = (1-v²)^1/2 and the time and space variables are expressed in the same units such that the constant (3)10⁸ meters/second equals unity. It follows that the one-way (not just the two-way) speed of light is invariant and isotropic with respect to any and every system of inertial coordinates.

Thus the propagation of light is isotropic with respect to the same class of coordinate systems in which mechanical inertia is isotropic. This is consistent with the fact that light itself is an inertial phenomena, e.g., it conveys momentum. In fact, the inertia of light can be seen as a common thread running through three of the famous papers published by Einstein in 1905. In the paper entitled "On a Heuristic Point of View Concerning the Production and Transformation of Light" Einstein advocated a conception of light as tiny quanta of energy and momentum, somewhat reminiscent of Newton's inertial corpuscles of light. It's clear that Einstein already understood that the conception of light as a classical wave is incomplete. In the paper entitled "Does the Inertia of a Body Depend on its Energy Content?" he explicitly advanced the idea of light as an inertial phenomenon, and of course this was suggested by the fundamental ideas of the special theory of relativity presented in the paper "On the Electrodynamics of Moving Bodies".

The Galilean conception of inertial frames assumed that all such frames share a unique foliation of spacetime into "instants". Thus the relation "in the present of" constituted an equivalence relation across all frames of reference. If A is in the present of B, and B is in the present of C, then A is in the present of C. However, special relativity makes it clear that there are infinitely many distinct loci of inertial simultaneity through any given event, because inertial simultaneity depends on the velocity of the worldline through the event. The inertial coordinate systems do induce a temporal ordering on events, but only a partial ordering. With respect to any given event we can still partition all the other events of spacetime into distinct causal regions, including "past", "present" and "future", but in addition we have the categories "future null" and "past null", and none of these constitute equivalence classes. For example, it is possible for A to be in the present of B, and B to be in the present of C, and yet A is not in the present of C. Being "in the present of" is not a transitive relation.

It could be argued that a total unique temporal ordering of events is a more useful organizing principle than the isotropy of inertia, and so we should adopt a class of coordinate systems that provides a total ordering. We can certainly do this, as Einstein himself described in his 1905 paper

The point of this "drawback" is that there is no physically distinguished "origin" on which to base the time coordination of all systems of reference, so from the standpoint of assessing possible causal relations we must still consider the full range of possible "absolute" temporal orderings. This yields the same partial ordering of events as does the set of inertial coordinates, so the "total ordering" that we can achieve by imposing a single temporal foliation on all frames of reference is only formal, and not physically meaningful. Nevertheless, we could make this choice, especially if we regard the total temporal ordering of events as a requirement of intelligibility. This seems to have been the view of Lorentz, who wrote in 1913 about the comparative merits of the traditional Galilean and the new Einsteinian conceptions of time

Of course, the idea of "arbitrarily large velocities" already pre-supposes a concept of absolute simultaneity, so Lorentz's rationale is not especially persuasive, but it expresses the point of view of an intellect that places great importance on a total temporal ordering, even at the expense of inertial isotropy. Indeed one of Poincare's criticisms of Lorentz's early theory was that it sacrificed Newton's third law of equal action and re-action. (This can be formally salvaged by assigning the unbalanced forces and momentum to an undetectable ether, but the physical significance of a conservation law that references undetectable elements is questionable.) Oddly enough, even Poincare sometimes expressed the opinion that a total temporal ordering would always be useful enough to out-weigh other considerations, and that it would always remain a safe convention.

The Galilean assumption as to the relation between relatively moving systems of inertial coordinates entails the assumption that speeds are arithmetically additive. Observations around the end of the 19th century revealed that the principles of relativity (of direction, position, and velocity) were empirically incompatible with the Galilean law of composition, so something had to be discarded. We may summarize the approach taken by Lorentz and most others by saying that they sacrificed the physical principles of inertial relativity, isotropy, and homogeneity in order to maintain the assumed Galilean composition law. This approach, although technically serviceable, suffers from a certain inherent lack of conviction, because while asserting the ontological reality of anisotropy in all but one (unknown) frame of reference, it unavoidably requires us to disregard that assertion and arbitrarily assume one particular frame as being "the" rest frame.

Poincare and Einstein recognized that in our descriptions of events in spacetime in terms of separate space and time coordinates we're free to select our "basis" of decomposition. This is precisely what one does when converting the description of events from one frame to another using Galilean relativity, but, as noted above, the Galilean composition law yields anisotropic results when applied to actual observations. So it appeared (to most people) that we could no longer maintain isotropy and homogeneity in all inertial frames together with the ability to transform descriptions from one frame to another by simply applying the appropriate basis transformation. But Einstein realized this was too pessimistic, and that the new observations were fully consistent with both isotropy in all inertial frames and with simple basis transformations between frames, provided we adjust our assumption about the effective metrical structure of spacetime. In other words, he brilliantly discerned that Lorentz's anisotropic results totally vanish in the context of a different metrical structure.

Even a metrical structure is conventional in a sense, because it relies on our ontological premises. For example, the magnitude of the interval between two events may seem to be one thing but actually be another, due (perhaps) to variations in our means of observation and measurement. However, once we have agreed on the physical significance of inertial coordinate systems, the invariance of the quantity (dt)² - (dx)² - (dy)² - (dz)² also becomes physically significant. This shows the crucial importance of the very first sentence in Section 1 of Einstein's 1905 paper:

To this Sommerfeld added the note "i.e., to the first approximation". This immediately establishes not only the convention of simultaneity, but also the means of operationally establishing it, and its physical significance. Any observer in any state of inertial motion can throw two identical billiard balls in opposite directions with equal force (i.e., so there is no net disturbance of the observer's state of motion), and the convention that those two objects have the same speed suffices to fully specify an entire system of space and time coordinates, which we call inertial coordinates. It is then an empirical fact - not a definition, convention, assumption, stipulation, or postulate - that the speed of light is isotropic with respect to inertial coordinates. This obviously doesn't imply that inertial coordinates are "true" in any absolute sense, but the principle of inertia has proven to be immensely powerful for organizing our knowledge of physical events, and for discerning and expressing the apparent chains of causation.

If a flash of light emanates from the geometrical midpoint between two spatially separate particles at rest in an inertial frame, the arrival times of the light wave at those two particles are simultaneous with respect to that inertial frame. It turns out that all other physical processes are isotropic with respect to inertial coordinates, e.g., if a sound wave emanates from the midpoint of a uniform steel beam at rest in an inertial frame, the sound reaches the two ends simultaneously in accord with this definition. If we adopt any other convention, we invariably introduce peculiar anisotropies, such as sound in a uniform stationary steel beam propagating more rapidly in one direction than in the other. The isotropy of physical phenomena - including the propagation of light - is strictly a convention, but it was not introduced by special relativity. It is one of the fundamental principles which we use to organize our knowledge, and it leads us to choose inertial coordinates for the description of events. The isotropy of physical phenomena with respect to inertial coordinates is not a convention, it is one of the defining attributes of inertial coordinates. The empirical fact that such a wide variety of phenomena are isotropic with respect to the same class of coordinate systems is evidence of the power and utility of inertia as an organizing principle.

To illustrate, imagine a spherical spaceship moving at high speed through empty space (without acceleration), with the air and everything else inside the spaceship moving right along with the ship, all at rest in the ship's rest frame. If we make a sound at the geometric center of the ship, the sound waves will start moving toward the walls at the speed of sound. Just before they reach the walls we turn on a light bulb at the geometric center of the ship, and the light wave starts moving toward the walls at the speed of light. Now, it's a matter of experimental fact that if the arrivals of the light and sound waves at one point on the wall coincide at a single event A, then their arrivals at the opposite point on the wall will also coincide at a single event B. The question of whether A and B are simultaneous cannot be empirically settled, but the fact that the coincidence of the arrivals in one direction implies their coincidence in all directions is an empirical fact. Now, by convention, we ordinarily agree that the natural decomposition of spacetime with respect to the spaceship's frame of reference is the one in which dynamical operations (including light waves, sound waves, mechanical inertia, and everything else) are isotropic. This leads us to adopt inertial coordinate systems.

Of course, we could, if we wish, maintain that A and B are not simultaneous, but then we need to realize that none of the physical processes inside the ship are isotropic. As light goes, so goes everything else. For example, if we decline to consider A and B as simultaneous, then it follows that if we tap the midpoint of a stationary steel beam inside the ship, the sound waves will not generally emanate to the two ends isotropically, unless we have the beam pointed in one particular direction. In fact, even the length of the beam will differ as it is pointed in different directions. In short, all of the physics inside the ship will be akimbo, and frankly there's little chance that we could keep it all straight, because as far as we can tell all the physics is working exactly the same as it would if the ship was moving at the same speed in the opposite direction! There is no reason for us to keep track of all these unobservable anisotropic "corrections" unless we're simply unwilling to accept the observed fact that different inertial frames have their own natural spacetime decompositions in which physics is isotropic.

So we've seen that although the principle of relativity constrains, it does not uniquely determine the form of the composition law for mapping results from one system of coordinates to another. In order to fix the observable elements of a spacetime theory with respect to every member of the equivalence class of inertial frames we require one further postulate, such as Einstein's operational light speed invariance discussed in Chapter 1.6 (or the dt � dx symmetry discussed in Chapter 1.9). However, we should distinguish between the strong and weak forms of the assumption of the light-speed invariance postulate. The strong form asserts that the one-way speed of light is invariant with respect to the natural space-time basis associated with any inertial state of motion, whereas the weak form asserts only that the round-trip speed of light is invariant.

To illustrate the different implications of these two different assumptions, consider an experiment of the type conducted by Michelson and Morley in their efforts to detect a directional variation in the speed of light, due to the motion of the Earth through the aether, with respect to which the absolute speed is light was presumed to be referred. To measure the speed of light along a particular axis they effectively measured the elapsed time at the point of origin for a beam of light to complete a round trip out to a mirror and back. At first we might think that it would be just as easy to measure the one-way speed of light, by simply comparing the time of transmission of a pulse of light from one location to the time of reception at another location, but of course this requires us to have clocks synchronized at two spatially separate locations, whereas it is precisely this synchronization that is at issue. Depending on how we choose to synchronize our separate clocks we can measure a wide range of light speeds. To avoid this ambiguity, we must evaluate the time interval for a transit of light at a single spatial location (in the coordinate system of interest), which requires us to measure a round trip, just as Michelson and Morley did.

Incidentally, it might seem that Roemer's method of estimating the speed of light from the variations in the period between eclipses of Jupiter's moons (see Section 3.3) constituted a one-way measurement, but in fact that method rests on an assumed synchronization between the "Jupiter clock" and clocks on the Earth, independent of the relative motion of the Earth. Since the relative speeds involved are quite small (in comparison with the speed of light), and the precision of measurement was quite rough, the issue of relativistic clock synchronization was insignificant for Roemer's calculation.

So, recognizing that we can only measure, without ambiguity, the lapses of time for closed-loop paths, it becomes clear that there is an unavoidable ambiguity in our interpretation of the relations between the times at separate spatial locations. We naturally prefer to assume inertially isotropic dynamics, and the isotropic case is within the ambiguity set, but it is not uniquely determined. The ambiguity arises because any over closed loop, by definition, the net change in each and every direction is zero. As a result, it is possible to consistently interpret all observations based on the assumption of non-isotropic physics. Admittedly the resulting laws take on a somewhat convoluted appearance, and contain unobservable parameters, but they can't be ruled out empirically.

This effect is significant only when we're making measurement that are accurate to the second order in v/c. Consider an experiment to measure the round-trip speed of light, and suppose we assume that light travels at a constant speed c relative to some absolute medium, with respect to which our laboratory is moving with a speed v. Under these assumptions, we would expect a pulse of light to travel with a speed c+v (relative to the lab) in one direction, and c-v in the opposite. So, if we send a beam of light over a distance L out to a mirror in the "c+v" direction, and it bounces back over the same distance in the "c-v" direction, then the total elapsed time to complete the round trip of length 2L is

Therefore, the average round-trip speed relative to the laboratory would be

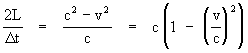
This shows why a round-trip measurement of the speed of light would not be expected to reveal any dependency on the velocity of the laboratory unless the measurement was precise enough to resolve second-order effects in v/c. The ability to detect such small effects was first achieved in the late 19th century with the development of precision interferometry. (It's interesting that the wave-like nature of light itself provided the means of detecting the invariance of light speed.)

The experiments of Michelson and Morley showed that, despite the movement of the Earth in its orbit around the Sun (to say nothing of the movement of the solar system, and even of the galaxy), there was no (v/c)² term in the round-trip speed of light. In other words, they found that 2L/D t is always equal to precisely c, at least to the accuracy they could measure, which was more than adequate to rule out a second-order deviation. Thus we have a firm empirical basis for asserting that the round-trip speed of light is independent of the motion of the source. This is the weak form of the invariant light speed postulate. However, in his 1905 paper, Einstein asserted the stronger claim, which is that we should regard the one-way speed of light as being invariant. This stronger postulate clearly doesn't follow from the results of Michelson and Morley, nor from any other conceivable experiment or observation. On the other hand, there is also no conceivable observation that could conflict with it. The invariant round-trip speed of light fixes the observable elements of the theory, but it does not uniquely determine the ontological structure, because multiple different interpretations can be made to fit the same set of appearances. The one-way speed of light is necessarily an interpretative element of our experience, consistent with our observations, but not uniquely so.

To illustrate the ambiguity, notice that we can ensure a null result for the Michelson and Morley experiment while maintaining non-constant light speed, merely by requiring that the speed of light v₁ and v₂ in the two opposite directions of travel (out and back) satisfy the relation

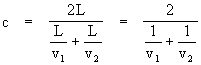
In other words, a linear round-trip measurement of light speed will yield the constant c in every direction provided only that the harmonic mean of the one-way speeds in opposite directions always equals c. This is easily accomplished, by defining the one-way velocity v₁ as a function of direction arbitrarily for all directions in one hemisphere, and then setting the velocities in the opposite directions the velocities v₂ in the opposite directions as v₂ = cv₁ / (2v₁ - c). However, we also wish to cover more complicated round-trips, rather than just back and forth on a single line. For example, to ensure that a circuit of light around an equilateral triangle with edges of length L yields a round-trip speed of c, the speeds v1, v2, v3 in the three equally spaced directions must satisfy

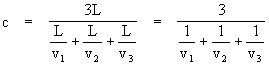
so again we see that the light speeds must have a harmonic mean of c. In general, to ensure that every closed loop of light, regardless of the path, yields the average speed c, it's necessary (and also sufficient) to have light speed v = C(q ) as a function of angle q in a principal plane such that, for any positive integer n,

In units with c = 1, we need the n terms on the left side to sum to n, so the velocity function must be such that 1/C(q ) = 1 + f(q ) where the function f(q ) satisfies

for all q . The canonical example of such a function is simply f(q ) = k cos(q ) for any constant k. Thus if we postulate that the speed of light varies as a function of the angle of travel q relative to some primary axis according to the equation

then we are assured that all closed-loop measurements of the speed of light will yield the constant c, despite the fact that the one-way speed of light is distinctly non-isotropic. No measurement can disprove the hypothesis that the one-way speed of light actually is (or is not) given by (1). It is, strictly speaking, a matter of convention. If we choose to believe that light has the same speed in all directions, then to send a synchronizing signal to two points we would locate ourselves midway between them (i.e., at the location where round trips between ourselves and those two points take the same amount of time.) On the other hand, if we choose to believe light travels twice as fast in one direction as in the other, we would locate ourselves 2/3 of the way between them (i.e., twice as far from one as the other, so round trip times are two to one). In either case we can synchronize all clocks according to our belief, and everything will be perfectly consistent and coherent. Of course, in any case it's necessary to account consistently for the lapse of time for information to get from one clock to another, but the lapse of time between any two clocks separated by a distance L can be anything we choose in the range from virtually 0 to 2L/c. The only real constraint is not on the speed of information in any particular direction, but on the shape of the speed as a function of spatial angle.

Specifically, notice that the velocity profile given by (1) is simply the polar equation of an ellipse (or ellipsoid is revolved about the major axis), with the pole at one focus, the semi-latus rectum equal to c, and eccentricity equal to k. This just projects the ellipse given by cutting the light cone with an oblique plane. Interestingly, there are really two light cones that intersect on this plane, and they are the light cones of the two events whose projections are the two foci of the ellipse - for timelike separated events. Recall that all rays emanating from one focus of an ordinary ellipse and reflecting off the ellipse will reconverge on the other focus, and that this kind of ray optics is time-symmetrical. In this context our projective ellipse is the intersection of two null-cones, i.e., it is the locus of all points in spacetime that are null-separated from both of the "foci events". This point of view makes the time-symmetry of Maxwell's equations (not to mention the relativistic Schrodinger equation) seem perfectly natural, as discussed in Section 9.

Our main reason for assuming k = 0 is our preference for symmetry, simplicity, and consistency with inertial isotropy. Within our empirical constraints, k can be interpreted as having any value between -1 and +1, but the principle of sufficient reason suggests that it should not be assigned a non-zero value in the absence of any rational justification. Nevertheless, it remains a convention (albeit a compelling one), but we should be clear about what precisely is conventional - and what is not. The invariance of lightspeed is a convention, but the invariance of lightspeed with respect to inertial coordinates is an empirical fact. Also, this empirical fact is not a formal tautology, because inertial coordinates are determined by mechanical inertia and Newton's laws of motion for material objects, independent of the propagation of light.

We'll see in subsequent sections that the standard formalism of general relativity provides a convenient means of expressing the relations between spacetime events with respect to a larger class of coordinate systems, so it may appear that inertial references are less significant in the general theory. In fact, Einstein once hoped that the general theory would not rely on the principle of inertia as a primitive element. However, this hope was not fulfilled, and the underlying physical basis of the spacetime manifold in general relativity remains the set of primitive inertial paths (geodesics) through spacetime. Not only do these inertial paths determine the equivalence class of allowable coordinate systems (up to diffeomorphism), it even remains true that at each event we can construct a (local) system of inertial coordinates with respect to which the speed of light is c in all directions. Thus the empirical fact of lightspeed invariance and isotropy with respect to inertial coordinates remains as a primitive component of the theory. The difference is that in the general theory the convention of using inertial coordinates is less prevalent, because in general there is no single global inertial coordinate system, and non-inertial coordinate systems are often more convenient on a curved manifold.

Return to Table of Contents