Since the special theory of relativity is a local theory, its natural objects of study are the absolute worldlines of individual particles, and it presuppose a preferred class of worldlines, those that represent inertial motion. The idea of a worldline is inherently absolute, since it is nominally defined with reference only to space and time, not to any other objects. A truly relational theory would take the "dual" approach, and regard the separations between objects as the most natural objects of study, leading to a relational theory to motion. In fact, one could go to the extreme of regarding separations as the primary ontological entities, and consider particles to be merely abstract concept that we use to psychologically organize those separations.
It's useful to explore this possibility, which we will do in this section from a (mostly) non-relativistic standpoint, and with the assumption of a flat metric, so that we can speak meaningfully about the unique separations between distant particles.
From this point of view the idea of "motion" is secondary, and we simply regard separations as abstract entities having certain properties that may vary with time. The relations and interactions between these entities are to be determined. In this context, rather than discussing inertial motion, we may discuss a class of separations that may be called the inertial separations. In Galilean spacetime we consider that each particle has some spatial position at each instant of absolute time, but we don't assume the existence of a preferred class of absolute worldlines. We insist on defining everything in terms of the relations between bodies.
The conventional idea of inertial worldlines leads immediately to absolute inertia, and a single body can be said to exhibit inertial motion, but if we restrict ourselves to inertial separations we have only a relational class, and so we can only talk about two (or more) bodies being in co-inertial motion. Is it possible to characterize the spatial separations that exist between co-inertial objects? This turns out to be slightly more subtle than one might suspect at first glance. For example, it might seem that the distance between two coinertial particles must vary as a linear function of time, but such a definition would exclude almost all inertial separations in the real world, because (for example) the distance s(t) between a stationary particle and a particle moving uniformly in a straight line through space does not generally vary linearly with time. We can see this clearly by considering an object moving tangentially relative to an observer as shown below:
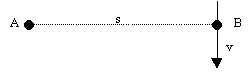
Obviously the separation between objects A and B in this configuration is stationary, i.e., we have ds/dt = 0 with respect to both objects' frames of references, and yet we know from experience that this configuration differs from one in which the two objects are at rest with respect to each other. For example, the Moon and Earth are separated by roughly a constant distance, and yet they are not at rest with respect to each other, because if they were the attraction of gravity would cause the separation to be reduced over time. We therefore, following Newton, describe motion not between objects, but between the extended non-rotating reference frames with respect to which those objects are at rest. Hence the characterization of inertial separations is more complicated than simply being linear functions of time. In fact, we will find that the condition for separations to be inertial is nearly identical to the condition for linear gravitational free-fall, as well as for certain other natural kinds of motion.
The three orthogonal components Dx, Dy, and Dz of the separation between two particles in unaccelerated motion relative to a common reference frame must be linear functions of time, i.e.,
where the coefficients ai and bi are constants. Therefore the magnitude of any "co-inertial separation" is of the form
where
Letting the subscript n denote nth derivative with respect to time, the first two derivatives of s(t) are
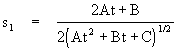
The right hand equation shows that s2 s03 = k, and we can differentiate this again and divide the result by s02 to show that the separation s(t) between any two particles in relatively unaccelerated (i.e., co-inertial) motion in Galilean spacetime must satisfy the differential equation
(1)
Now, suppose we consider the separation that characterizes an isolated non-rotating two-body system in gravitational free-fall. Assume the two bodies are identical particles, each of mass m. According to Newtonian theory the inertial and gravitational constraints are coupled together by the auxiliary quantity called "force" by the following equations
where G is a universal constant. (Note that each particle's "absolute" acceleration is one half of the second derivative of their mutual separation with respect to time.) Equating these two forces gives 
. Differentiating this again and dividing by s0, we can characterize non-rotating gravitational free-fall by the purely kinematic equation
(2)
The formal similarity between equations (1) and (2) is remarkable, considering that the former describes strictly inertial separations and the latter describes gravitational separations. We can show how the two are related by considering general free motion in a gravitational field. The Newtonian equations of motion are
where r is the magnitude of the distance from the center of the field and w is the angular velocity of the particle. If we solve the left hand equation for w and differentiate to give dw/dt, we can substitute these expressions into the right hand equation and re-arrange the terms to give
which applies (in the Newtonian limit) to arbitrary free paths of test particles in a gravitational field. Obviously if m = 0 this reduces to the free inertial separations, whereas for purely radial motion we have d2r/dt2 = -m/r2, and so this reduces to the equation for radial gravitational separation.
Now suppose a particle of mass m is attached to a rod in such a way that it can slide freely along the rod. If we rotate the rod about some point P then the particle in general will tend to slide outward along the rod away from the center of rotation in accord with the basic equation of motion
where s is the distance from the center of rotation to the sliding particle and w is the angular velocity of the rod. The general solution of this equation is
where A and B are constants determined by the initial conditions. Setting s(0) = r0 and s1(0) = v0, we have
Substituting these coefficients into the expression for s(t) gives
From this it follows that s(t) satisfies the equation
(3)
So, we have found that arbitrary co-inertial separations, non-rotating gravitational separations, and rotating radial separations are all characterized by a differential equation of the form
(4)
for some constant N. Notice that among the other solutions of this equation (with N = -1) are the elementary transcendental functions et, sin(t), and cos(t). Solving for N so as to isolate the arbitrary constant we have
Differentiating this gives the basic equation
where subscripts now denote derivatives with respect to time. If none of s0, s1, s2, and s3 is zero we can divide by all of these to give the interesting form
Incidentally, even though the above has been based on the Galilean spatial separations between objects as a function of Galilean time, the same conditions can be shown to apply to the absolute spacetime intervals between inertial particles as a function of their proper times. Relative to any point on the worldline of one particle, the four components Dt, Dx, Dy, and Dz of the absolute interval to any other inertially moving particle are all linear functions of the proper time t along the latter particle's worldline. Therefore, the components can be written in the form
where the coefficients ai and bi are constants. It follows that the absolute magnitude of any "co-inertial separation" is of the form
where
Thus we have formally the same dependence as before, except now the parameter s represents the absolute spacetime separation. This shows that the absolute separation between any fixed point on one inertial worldline and a point advancing along any other inertial worldline satisfies the equation where subscripts denote derivatives with respect to proper time of the advancing point. Naturally the dual relation also holds, as well as the absolute separation between two points, each advancing along arbitrary inertial worldlines, correlated according to their respective proper times.