4.1 Immovable Spacetime

Although the words "relativity" and "relational" share a common root word, their meanings are very different. The principle of relativity asserts that each inertial frame of reference possesses it own natural (i.e., isotropic and homogeneous) measures of time and space, so that the natural decomposition of spacetime intervals into temporal and spatial components can be defined only relative to some particular frame of reference. Of course, the absolute spacetime intervals themselves are invariant, so the "relativity" refers only to the natural decomposition (analysis) of these intervals. (This decomposition could be regarded as merely conventional, except for the empirical fact that the quantum phases of objects evolve in proportion to the "natural" temporal coordinates prescribed by relativity.) In contrast, the principle of relationalism asserts that the absolute intervals between material objects fully characterize their extrinsic positional status, without reference to any underlying non-material system of reference which might be called "absolute space".

We should note that the traditional debate between relational and absolute motion is of questionable relevance in the context of a physics that recognizes continuous fields as physical entities, because fields permeate all of space, so there are no longer any unoccupied locations. Thus every point in the entire spacetime manifold is a vertex of actual relations between physical entities, which obscures the distinction between absolute and relational premises. Furthermore, in the context of the general theory of relativity, spacetime itself is a field, i.e., a physical entity, which not only acts upon material objects but is also acted upon by them, so the absolute-relational distinction may seem to disappear totally. However, it remains possible to regard fields as only representations of effects, and to insist on materiality for ontological objects, in which case the absolute-relational question remains both relevant and unresolved.

Of course, there has always been a strong desire among physicists to make their theories relational, but they have always run into the same problem, namely, acceleration in general, and rotation in particular. For example, Newton struggled with the fact that the Moon is relationally stationary with respect to the Earth, and yet if a massive stationary object is simply floating above the Earth and subject to a force of attraction, it should very quickly crash down on us. What is holding the Moon up? Or, to put the question differently, why is the Moon not accelerating directly toward the Earth in accord with the gravitational force that is presumably being applied to it?

Newton's brilliant answer was that the Moon is accelerating directly toward the Earth, and with precisely the magnitude of acceleration predicted by his gravity formula. But if the Moon is constantly accelerating directly toward the Earth, why doesn't it ever get here? According to Newton (and no less in the theory of relativity) the Moon is moving relative to the Earth, but perpendicularly to the Earth-Moon axis, with a velocity v = wR, where R is the Earth-Moon distance and w is the Moon's angular velocity, i.e., roughly 2p radians/moonth. Of course, if left to it's own devices, the Moon would just wander off tangentially away from the Earth, but the force of gravity is modifying its velocity by adding GM/R² ft/sec per second each second toward the Earth, which causes the Moon to turn continually in a roughly circular orbit around the Earth. The centripetal acceleration of an object revolving in a circle is v² / R = w² R, and so (Newton reasoned) this must equal the gravitational acceleration. Thus we have w² R³ = GM, which of course Kepler's third Law. The crucial point is that the explanation depends on strictly non-relational concept of motion. In fact, it might be said that this was the crucial insight of Newtonian dynamics - and it applies no less in special relativity. For the purposes of dynamical analysis, motion must be referred to an absolute background class of rectilinear inertial coordinate systems, rather than simply to the relations between (local) material bodies, or even classical fields. Thus we can not infer everything important about an object's state of motion simply from its distances from nearby objects. In this sense, both Newtonian and relativistic physics find it necessary to invoke absolute space.

The concept of absolute space presents us with an ontological puzzle, because we can empirically verify the physical equivalence of all uniform states of motion, which suggests that position and velocity have no absolute physical significance, and yet we can also verify that changes in velocity (i.e., accelerations) do have absolute significance, independent of the relations between material bodies (at least in a local sense). If the evident relativity of position and velocity lead us to discard the idea of absolute space, then how are we to understand the apparent absoluteness of acceleration? Some have argued that in order for the change in something to be ontologically real, it is necessary for the thing itself to be real, but of course that's not the case. It's perfectly possible for "the thing itself" to be an artificial conception, whereas the "change" is the ontological entity.

For example, the Newtonian concept of the physical world was of a set of particles, between which relations existed. The primary ontological entities were the particles, but it's equally possible to imagine that the separations are the "real" entities, and particles are merely relations between separations, i.e., particles are a convenient bookkeeping device for organizing the facts of a set of separations. This raises some interesting questions, such as whether an unordered multiset of n(n-2)/2 separations suffices to uniquely determine a configuration of n points in a space of fixed dimension. It isn't difficult to find examples of multisets of separations that allow for multiple distinct spatial arrangements. For example, given the multiset of ten separations

we can construct either of the two five-point configurations shown below

For another example, the following three distinct configurations of eight co-planar points each have the same set of 28 point-to-point separations:

In fact, of the 12870 possible arrangements of eight points on a 4x4 grid, there are only 1120 distinct multisets of separations. Of course, much of this reduction is due to rotations and reflections, but not all. Spatially distinct configurations of points with the same multiset of distances are not uncommon. They are sometimes called isospectral sets, referring to the spectrum of point-to-point distances.

Examples such as these may suggest that unordered separations cannot be the basis of our experience, although we can't, a priori, rule out the possibility that our interpretation of experience is non-unique, and perhaps different states of consciousness might perceive a given physical configuration differently. We normally require the elements of a physical theory to uniquely determine only the observables, rather than our interpretations, but some of our most fundamental interpretations (such as the belief in objects rather than separations as primary entities) are difficult to isolate from the act of observation. In any case, if we reject the of non-unique mapping to our conventional domain of objects, we can still imagine a separation-based ontology by stipulating on ordering for those separations. We consider in Chapter 4.2 the form which laws of separation might take.

According to both Galilean and Einsteinian (special) relativity, position and velocity are relative but acceleration is not, and this is explained by asserting that the set of all possible systems of reference can be partitioned into equivalence classes, such that two systems are in the same class if and only if the coordinates of an object at rest in one system are constant linear functions with respect to the other system. Furthermore, there is one particular equivalence class of reference systems that is physically distinguished from all the others, and we call this preferred class the inertial coordinate systems. According to classical and special relativity, the inertial coordinate systems are symmetrical, and each one is physically equivalent. In particular, we cannot single out one particular inertial system and claim that it is the "central" frame, because the equivalence class has no center, and all ontological qualities are uniformly distributed over the entire class.

From a purely formal standpoint, the purported uniform distribution over inertial frames is problematical, because the inertial systems of reference along a single line can only be linearly parameterized in terms of a variable that ranges from -� to +� , such as q = log((1+v)/(1-v)), but if each value of q is to be regarded as equally probable, then we are required to imagine a perfectly uniform density distribution over the real numbers. The problem is that, mathematically, no such distribution exists. To illustrate, try to imagine selecting a number randomly from a uniform distribution of all the real numbers. This is the source of many interesting mathematical conundrums, such as the "High-Low Number" strategy game, whose answer depends on the fact that no perfectly uniform distribution exists over the real numbers (nor even over the integers). If, like Einstein, we are interested in whether there was any arbitrary choice in the creation of the physical world, we see that the selection of our particular rest frame cannot have been perfectly arbitrary from a set of pre-existing alternatives.

These considerations lead to the views expressed by Mach and others, that the only intelligible way to imagine the existence of objects all in roughly the same frame of reference within a perfectly symmetrical class of possible reference systems is to imagine that the objects themselves are in some way responsible for the class. In other words, we must have complete relationalism. Unfortunately, no completely successful relational theory of motion has ever been devised (although there have been some interesting attempts, cf., Barbour and Bertotti).

One common feature of purely relational models is evidently non-locality, because there seems to be no way, if we limit ourselves to local observations, to identify the inertial motions of material objects purely from the kinematical relations between them. We're forced to attribute the distinction between inertial and non-inertial motion to some non-material (or non-local) interaction. This is nicely illustrated by Einstein's thought experiment (based on Newton's famous "spinning pail") involving two nominally identical fluid globes S₁ and S₂ floating in an empty region of space. One of these globes is set rotating (about their common axis) while the other remains stationary. The rotating globe assumes an oblate shape due to its rotation.

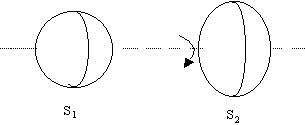
If globes are mutually stationary and not rotating, they are both spherical and symmetrical, and we cannot distinguish between them. However, if one of the globes is spinning about their common axis, the principle of inertia leads us to expect that the spinning globe will bulge at the "equator" and shrink along its axis of rotation due to the centripetal forces. The "paradox" (for the relationalist) is that each globe is spinning with respect to the other, so they must still be regarded as perfectly symmetrical, and yet their shapes are no longer congruent. To what can we attribute the asymmetry?

If we look further afield we may notice that the deformed globe is rotating relative to all the distant stars, whereas the spherical globe is not. A little experimentation shows that a globe's deformation is strictly a function of its speed of rotation relative to the distant stars, and presumably this is not a mere coincidence. Of course, Newton's explanation for this coincidence was to argue that the local globes and the distant stars all reside in the same absolute space, and it is this space that defines absolute (inertial) motion, and likewise the special relativistic theory invokes an absolutely preferred class of reference frames. Moreover, in the general theory of relativity, when viewed from a specific cosmological perspective, there is always a preferred frame of reference, owing to the global boundary conditions that must be imposed in order to single out a solution. This came as a shock to Einstein himself at first, since he was originally thinking (hoping) that the field equations of general relativity represented true relationalism, but his conversion began when he received Schwarzschild's exact solution for spherical symmetry, which of course exhibits a preferred coordinate system such that the metric coefficients are independent of time, i.e., the usual Schwarzschild coordinates, which are essentially unique for that particular solution.

Likewise for any exact solution we can name there is some globally unique system of reference singled out by symmetry or boundary conditions (even for asymptotically flat universes, as Einstein himself showed). For example, in the Friedman "big bang" cosmologies there is a preferred global system of coordinates corresponding to the worldlines with respect to which the cosmic background radiation is isotropic. Of course, this is not a fresh insight. The non-relational global aspects of general relativistic cosmologies have been extensively studied, beginning with Einstein's 1917 paper on the subject, and continuing with Goedel's rotating empty universes, and so on. Such examples make it clear general relativity is not a relational theory of motion. In other words, general relativity does not correlate all physical effects with the relations between material bodies, but rather with the relations between objects (including fields) and the absolute background metric, which is affected by, but is not determined by, the distribution of objects (except arguably in closed cosmological models). Thus, relativity, no less than Newtonian mechanics, relies on spacetime as an absolute entity in itself, exerting influence on fields and material bodies. The extra information contained in the metric of spacetime is typically introduced by means of boundary conditions or "initial values" on a spacelike foliation, sufficient to fix a solution of the field equations.

Thus, relativity very quickly disappointed its early logical-positivist supporters when it became clear that it was not, and never had been, a relational theory of motion, ala Leibniz, Berkeley, or Mach. Initially even Einstein was "scandalized" by the Schwarzschild and de Sitter solutions, which represent complete metrical manifolds with only one material object or none at all (respectively). These examples made it clear that spacetime in the theory of relativity could not simply be regarded as the totality of the extrinsic relations between material objects (and non-gravitational fields), but is a primary physical entity of the theory, with its own absolute properties, most notably the metric with its related invariants, at each point.

Indeed this was Einstein's eventual answer to Mach's critique of pre-relativity physics. Mach had complained that it was unacceptable for our theories to contain elements (such as spacetime) that act on (i.e., have an effect on) other things, but that are not acted upon by other things. Mach, and the other relationalists before him, naturally expected this to be resolved by eliminating spacetime, i.e., by denying that an entity called "spacetime" acts in any physical way. To Mach's surprise (and unhappiness), the theory of relativity actually did just the opposite - it satisfied Mach's criticism by instead making spacetime a full-fledged element of theory, acted upon by other objects. By so doing, Einstein believed he had responded to Mach's critique, but of course Mach hated it, and said so. Early in his career, Einstein was sympathetic to the idea of relationism, and entertained hopes of banishing absolute space from physics but, like Newton before him, he was forced to abandon this hope in order to produce a theory that satisfactorily represents our observations.

The absolute significance of spacetime in the theory of relativity was already obvious from trivial considerations of the special theory. The twins paradox is a good illustration of why relativity cannot be a relational theory, because the relation between the twins is perfectly symmetrical, i.e., the spatial distance between them starts at zero, increases to some maximum value, and then decreases back to zero. The distinction between the twins cannot be expressed in terms of their mutual relations to each other, but only in terms of how each of their individual worldlines are embedded in the absolute metrical manifold of spacetime. This becomes even more obvious in the context of general relativity, because we can then have multiple distinct geodesic paths between two given events, with different lapses of proper time, so we cannot even appeal to any difference in "felt" accelerations or local physics of any kind to account for the asymmetry.

Hopes of accounting for this asymmetry by reference to the distant stars, ala Mach, were certainly not fulfilled by general relativity, according to which the metric of spacetime is conditioned by the presence of matter, but only to a very slight degree in most circumstances. From an overall cosmological standpoint we are unable to attribute the basic inertial field to the configuration of mass and energy, and we have no choice but to simply assume a plausible absolute inertial background field, just as in Newtonian physics, in order to actually make predictions and solve problems. This is necessarily a separate and largely independent stipulation from our assumed distribution of matter and energy.

It's interesting to note that Galilean relativity is actually more relational than special relativity. This is essentially because the unified spacetime manifold with the lightcone structure of Minkowski spacetime is more rigid than a pure Cartesian product of a three-dimensional spatial manifold and an independent one-dimensional temporal manifold. In Galilean spacetime at a spatial point P₀ and time t₀ there is no restriction at all on the set of spatial points at t₀ + dt that may "spatially coincide with P₀" with respect to some valid inertial frame of reference. In other words, an inertial worldline through P₀ at time t₀ can pass through any point in the entire universe at time t₀ + dt for any positive dt. In contrast, the lightcone structure of Minkowski spacetime restricts the future of the point P₀ to points inside the future null cone, i.e., P₀ � cdt, and as dt goes to zero, this range goes to zero, imposing a well-defined unique connection from each "infinitesimal" instant to the next, which of course is what the unification of space and time into a single continuum accomplishes.

We referred above to Newtonian spacetime without distinguishing it from what has come to be called Galilean spacetime. This is because Newton's laws are manifestly invariant under Galilean transformations, and in view of this it would seem that Newton should be counted as an advocate of relativistic spacetime. However, in several famous passages of the first Scholium of the Principia Newton seems to reject the very relativity on which his physics is founded, and to insist on distinctly metaphysical conceptions of absolute space and time. He wrote

It isn't trivial to unpack the intended significance of these statements, especially because Newton has supplied three alternate names for each of the two types of quantities that he wishes us to distinguish. On one hand we have absolute, true, mathematical quantities, and on the other we have relative, apparent, common quantities. The latter are understood to be founded on our sense perceptions, so the former presumably are not, which seems to imply that they are metaphysical. However, Newton also says that this distinction is useful for dispelling certain prejudices, which suggests that his motives are utilitarian and/or pedagogical rather than to establish an ontology. He continues

Newton's insistence on the necessity of referring all true motions to "immovable space" has often puzzled historians of science, because his definition of absolute space and time are plainly metaphysical, and it's easy to see that Newton's actual formulation of the laws of physics is invariant under Galilean transformations, and the concept of absolute space plays no role. Indeed, each mention of a "state of rest" in the definitions and laws is accompanied by the phrase "or uniform motion in a right line", so the system built on these axioms explicitly does not distinguish between these two concepts. What, then, did Newton mean when he wrote that true motions must be referred to immovable space?

The introductory Scholium ends with a promise to explain how the true motions of objects are to be determined, declaring that this was the purpose for which the Principia was composed, so it's all the more surprising when we find that the subject is never even mentioned in Books I or II. Only in the concluding Book III, "The System of the World", does Newton return to this subject, and we finally learn what he means by "immovable space". Although his motto was "I frame no hypotheses" we find, immediately following Proposition X in Book III (in the third edition), the singular hypothesis

HYPOTHESIS I: That the centre of the system of the world is immovable.

In support of this remarkable assertion, Newton simply says "This is acknowledged by all, although some contend that the earth, others that the sun, is fixed in that centre." In the subsequent proposition XI we finally discover Newton's immovable space. He writes

PROPOSITION XI: That the common centre of gravity of the earth, the sun, and all the planets, is immovable. For that centre either is at rest or moves uniformly forwards in a right line; but if that centre moved, the center of the world would move also, against the Hypothesis.

This makes it clear that Newton's purpose all along has been not to deny Galilean relativity or the fundamental principle of inertia, but simply to show that a suitable system of reference for determining true inertial motions need not be centered on some material body. This was foreshadowed in the first Scholium when he wrote "it may be that there is no body really at rest, to which the places and motions of others may be referred". Furthermore, he notes that many people believed the immovable center of the world was at the center of the Earth, whereas others followed Copernicus in thinking the Sun was the immovable center. Newton evidently (and rightly) regarded it as one of the most significant conclusions of his deliberations that the true inertial center of the world was in neither of those objects, but is instead the center of gravity of the entire solar system. We recall that Galileo found himself in trouble for claiming that the Earth moves, whereas both he and Copernicus believed that the Sun was absolutely stationary. Newton showed that the Sun itself moves, as he continues

This was certainly a magnificent discovery, worthy of being called the purpose for which the Principia was composed, and it is clearly what Newton had in mind when he wrote the introductory Scholium promising to reveal how immovable space (i.e., the center of the world) is to be found.

In this context we can see that Newton was not claiming the ability to determine absolute rest, but rather the ability to infer from phenomena a state of absolute inertial motion, which he identified with the center of gravity of the solar system. He very conspicuously labels as a Hypothesis (one of only three in the final edition of the Principia) the conventional statement, "acknowledged by all", that the center of the world is immovable. By these statements he was trying to justify calling the solar system's inertial center the center of the world, while specifically acknowledging that the immovability of this point is conventional, since it could just as well be regarded as moving "uniformly forwards in a right line".

The modern confusion over Newton's first Scholium arises from trying to impose an ontological interpretation on a 17th century attempt to isolate the concept of pure inertia, and incidentally to locate the "center of the world". It was essential for Newton to make sure his readers understood that "uniform motion" and "right lines" cannot generally be judged with reference to neighboring bodies (such as the Earth's spinning surface), because those bodies themselves are typically in non-uniform motion. Hence he needed to convey the fact that the seat of inertia is not the Earth's center, or the Sun, or any other material body, but is instead absolute space and time - in precisely the same sense that spacetime is absolute in special relativity. This is distinct from asserting an absolute state of rest, which Newton explicitly recognized as a matter of convention.

Indeed, we now know the solar system itself revolves around the center of the galaxy, which itself moves with respect to other galaxies, so under Hypothesis I we must conclude that Proposition XI is strictly false. Nevertheless, the deviations from true inertial motion represented by those stellar and galactic motions are so slight that Newton's "immovable center of the world" is still suitable as the basis of true inertial motion for nearly all purposes. In a more profound sense, the concept of "immoveable space" been carried over into modern relativity because, as Einstein said, spacetime in general relativity is endowed with physical qualities that enable it to establish the local inertial frames, but "the idea of motion may not be applied to it".