3.2 Natural and Violent Motions

The concept of force is one of the most peculiar in all of physics, and has a fascinating history. It is, in one sense, the most viscerally immediate concept in classical mechanics, and seems to serve as the essential "agent of causality" in all interactions, and yet the ontological status of force has always been highly suspect. For example, we intuitively regard force as the cause of changes in motion, and imagine that those changes would not occur in the absence of the forces, but this causative aspect of force is an independent assumption that does not follow from any quantifiable definition, since we could equally well regard force as being caused by changes in motion, or even as merely a descriptive parameter with no independent ontological standing at all.

In addition, there is an inherent ambiguity in the idea of changes in motion, because it isn't obvious what constitutes unchanging (i.e., unforced) motion. Aristotle found it necessary to distinguish between two fundamentally distinct kinds of motion, which he called natural motions and violent motions. The natural motions included the apparent movements of celestial objects, the falling of leaves to the ground, the upward movement of flames and hot gases in the atmosphere, or of air bubbles in water, and so on. According to Aristotle, the cause of such motions was that all objects and substances have a natural place or level (such as air above, water below), and they proceed in the most direct way, along straight vertical paths, to their natural places. The motion of the celestial bodies was circular because this was the most perfect kind of unchanging motion, whereas the necessarily transitory motions of sublunary objects were rectilinear. It may not be too misleading to characterize Aristotle's concept of sublunary motion as a theory of buoyancy, since the natural place of light elements is above, and the natural place of heavy elements is below. If an object is out of place, it naturally moves up or down as appropriate to reach its proper place.

Aristotle has often been criticized for saying (or seeming to say) that the speed at which an object falls (through the air) is proportional to its weight. To the modern reader this seems absurd, and is contradicted by the simplest observations of falling objects. However, it's conceivable that we misinterpret Aristotle's meaning, partly because we're so accustomed to regarding the concept of force as the cause of motion, rather than as an effect or concomitant attribute of motion. If we consider the downward motive force (which Aristotle would call the weight) of an object to be the force required to keep it at its current height, then the "weight" of an object really is substantially greater the faster it falls. Some Aristotelian scholars have speculated that this was Aristotle's actual meaning, although his writing's on the subject are so sketchy that we can't know for certain. In any case, it illustrates that the concept and significance of force in a physical theory is often murky, and it also shows how thoroughly our understanding of physical phenomena is shaped by the distinction between forces (such as gravity) that we consider to be causes of motion, and those (such as impact forces) that we consider to be caused by motion.

Aristotle also held that the speed of motion was not only proportional to the "weight" (whatever that means) but inversely proportional to the resistance of the medium. Thus his proposed law of motion could be expressed roughly as V = W/R. He used this to argue against the possibility of empty space, i.e., regions in which R = 0, because the velocity of any object in such a region would be infinite. This doesn't seem like a very compelling argument, since we could easily counter that the putative vacuum would not be the natural place of any object, so it would have no "weight" in that direction either. Nevertheless, perhaps to avoid wrestling with the mysterious fraction 0/0, Aristotle surrounded the four sublunary elements of Earth, Water, Air, and Fire with a fifth element (quintessence), the lightest of all, called aether. This aether filled the super-lunary region, ensuring that we would never need to divide by zero.

In addition to natural motions, Aristotle also considered violent motions, which were any motions resulting from acts of volition of living beings. Although his writings are somewhat obscure and inconsistent in this area, it seems that he believed such beings were capable of self-motion, i.e., of initiating motion in the first instance, without having been compelled to motion by some external agent. Such self-movers are capable of inducing composite motions in other objects, such as when we skip a stone on the surface of a pond. The stone's motion is compounded of a violent component imparted by our hand, and natural components of motion toward its natural place (below the air and water). However, as always, we must be careful not to assume that this motion is to be interpreted as the causative result of the composition of two different kinds of forces. It was, for Aristotle, simply the kinematic composition of two different kinds of motion.

The bifurcation of motion into two fundamentally different types, one for natural motions of non-living objects and another for acts of human volition, and the attention that Aristotle gave to the question of unmoved movers, etc., is obviously related to the issue of free will, and demonstrates the strong tendency of scientists in all ages to exempt human behavior from the natural laws of physics, and to regard motions resulting from human actions as original, in the sense that they need not be attributed to other motions. We'll see in Section 9 that Aristotle's distinction between natural and violent motions plays a key role in the interpretations of certain puzzling aspects of quantum theory.

We can also see that the ontological status of "force" in Aristotle's physics is ambiguous. In some circumstances it seems to be more an attribute of motion rather than a cause of motion. Even if we consider the quantitative physics of Galileo, Newton, and beyond, it remains true that "force", while playing a central role in the formulation, serves mainly as an intermediate quantity in the calculations. In fact, the concept of 'force' could almost be eliminated entirely from classical mechanics. Newton wrestled with the question of whether force should be regarded as an observable or simply a relation between observables. Interestingly, Ernst Mach regarded the 3rd Law as Newton's most important contribution to mechanics, even though other's have criticized it as being more a definition than a law.

Newton struggle to find the "right" axiomatization of mechanics can be seen by reading the preliminary works he wrote leading up to The Principia, such as "De motu corporum in gyrum" (On the motion of bodies in an orbit). At one point he conceived of a system with five Laws of Motion, but what finally appeared in Principia were eight Definitions followed by three Laws. He defined the "quantity of matter" as the measure arising conjointly from the density and the volume. In his critical review of Newtonian mechanics, Mach remarked that this definition is patently circular, noting that "density" is nothing but the quantity of matter per volume. However, all definitions ultimately rely on undefined (irreducible) terms, so perhaps Newton was entitled to take density and volume as two such elements of his axiomatization. Furthermore, by basing the quantity of matter on explicitly finite density and volume, Newton deftly precluded point-like objects with finite quantities of matter, which would imply the existence of infinite forces and infinite potential energy according to his proposed inverse-square law of gravity.

The next basic definition in Principia is of the "quantity of motion", defined as the measure arising conjointly from the velocity and the quantity of matter. Here we see that "velocity" is taken as another irreducible element, like density and volume. Thus, Newton's ontology consists of one irreducible entity, matter, possessing the three primitive attributes density, volume, and velocity, and then defines two secondary attributes, the "quantity of matter" (which we call "mass") as the product

mass = (density)(volume)

and the "quantity of motion" (which we call "momentum") as the product

momentum = (velocity)(mass) = (velocity)(density)(volume)

Although Newton refers to this as a "quantity", suggesting a scalar, we know that velocity is a vector, (i.e., it has a magnitude and a direction), so it's clear that momentum also is a vector. After going on to define various kinds of forces and attributes of those forces, Newton then, as we saw in Section 1.3, took the law of inertia and relativity as his First Law of Motion, just as Descartes and Huygens had done. Following this we have the "force law", i.e., Newton's Second Law of Motion, which was expressed in the Principia as follows:

Notice that this statement doesn't agree precisely with either of the two forms in which the Second Law is commonly given today, namely, as F = dp/dt or F = ma. The former is perhaps closer to Newton's actual statement, since he did express the law in terms of momentum rather than acceleration, but he didn't refer to the rate of change of momentum. No time parameter appears in the statement at all. This is actually symptomatic of a confusion that had existed since at least the time of Aristotle, over the distinction between "impulse force" and "continuous force". Recall that our speculative interpretation of Aristotle's downward "weight" was based on the idea that he actually had in mind something like the impulse force that would be exerted by the object if it were abruptly brought to a halt. Newton's Second Law, as expressed in the Principia, seems to refer to such an impulse, and this is how Newton used it in the first few Propositions. However, he soon began to invoke the Second Law with respect to continuous forces of finite magnitude applied over a finite length of time (more in keeping with a continuous force of gravity, for example). This shows that even in the final version of the axioms and definitions laid down by Newton, he did not completely succeed in clearly delineating the concept of force that he had in mind. Of course, in each application of the Second Law, Newton made the necessary dimensional adjustments to appropriately account for the temporal aspect that was missing from the statement of the Law itself. (His ability to reliably incorporate these factors in each context testifies to his solid grasp of the new dynamics, despite the imperfections of his formal articulation of it.)

Soon after reading Einstein's 1905 paper on special relativity, Max Planck undertook to reconcile Newton's laws of motion within the relativistic framework, and found it convenient to work with the formulation F = dp/dt. However, in the modern formulation of relativistic mechanics, the concept of force is largely an anachronism, and its various generalized definitions are introduced mainly for the purpose of relating relativistic descriptions to their classical counterparts.

The third Law of Motion in the Principia is widely regarded as one of Newton's greatest and most original contributions to physics. This law states that

The word "action" is not found among the previously defined terms, but in the subsequent text Newton clarifies the intended meaning. He says "If a body impinge upon another, and by its force change the motion of the other, that body also... will undergo an equal change in its own motion towards the contrary part." In other words, the net change in the "quantity of motion" (i.e., the sum of the momentum vectors) is zero, so momentum is conserved. More subtly, Newton observes that "If a horse draws a stone tied to a rope, the horse will be equally drawn back towards the stone". This is true even if neither the horse nor the stone are moving (which of course implies that they are each subject to other forces as well, tending to hold them in place). The illustrates how the concept of force enables us to conceptually decompose a null net force into non-null components, each representing the contributions of different physical interactions.

It may be best to regard Newton's three "laws of motion" as actually comprising the definition of an inertial coordinate system. From this point of view the first law imposes the requirement that the spatial coordinates of any material object free of external forces are linear functions of the time coordinate, which is to say, free objects move with a uniform speed in a straight line with respect to an inertial coordinate system. Rather than seeing this is a law governing the motions of free objects with respect to a given system of coordinates, it is more correct to regard this as defining a class of coordinates systems, in terms of which a recognizable class of motions have particularly simple descriptions. The first law serves to fix the shape of the coordinate axes, but it does not fully define a system of inertial coordinates, because the first law is satisfied in infinitely many systems of coordinates that are not inertial. The system of oblique xt coordinates illustrated below is an example of such a system.

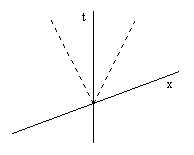
The two dashed lines indicate the paths of two identical objects, both initially at rest with respect to these coordinates and propelled outward from the origin by impulses forces of equal magnitude. Every object not subject to external forces moves with uniform speed in a straight line with respect to this coordinate system, so Newton's First Law of motion is satisfied, but the second law clearly is not, because the speeds imparted to these identical objects by equal forces are not equal. In other words, inertia is not isotropic with respect to these coordinates. In order for Newton's Second Law to be satisfied, we not only need the coordinate axes to be straight and uniformly graduated relative to freely moving objects, we need the space axes to be aligned in time such that mechanical inertia is the same in all spatial directions (so that, for example, the objects whose paths are represented by the two dashed lines in the above figure have the same speeds). This effectively establishes the planes of simultaneity of inertial coordinate systems. In an operational sense, Newton's Third Law is also involved in establishing the planes of simultaneity for an inertial coordinate system, because it is only by means of the Third Law that we can actually define "equal forces" as the forces necessary to impart equal "quantities of motion".

Overall, Newton's laws of motion essentially constitute the definition of inertial coordinate systems. One common misunderstanding of inertial coordinate systems is that they are fully characterized by the First Law, i.e., by the requirement that free objects move uniformly in a straight line. It's easy to overlook the fact that inertial coordinate systems are also required (by the Second and Third Laws) to have isotropic inertia, and this unambiguously determines the planes of simultaneity. This enables us to establish inertial coordinate systems purely by mechanical means, and then (for example) experimentally evaluate the propagation speed of light in terms of these coordinate systems. When we perform such experiments, in more or less arbitrarily selected inertial coordinate systems, we invariably find the speed of light to have the same value and to be independent of spatial direction. This is the empirical basis for the inference that the speed of light is invariant and isotropic with respect to every system of inertial coordinates.

Of course, this doesn't imply that inertial coordinate systems are the "true" systems of reference. They are simply the most intuitive, convenient, and readily accessible systems, based on the inertial behavior of material objects. Some readers might wonder how we can unequivocally assert the isotropy of the one-way speed of light. Are not all measurements of lightspeed really two-way measurements? Does not a one-way measurement require us to specify, independently, a synchronization of spatially separate clocks, and therefore planes of simultaneity? Yes, it does, and the isotropy of mechanical inertia with respect to inertial coordinates provides the independent physical basis for specifying the planes of simultaneity. Hence when we say the one-way speed of light is invariant and isotropic with respect to inertial coordinate systems, we are actually making the empirically verifiable claim that the propagation of light is isotropic with respect to precisely the same class of coordinate systems (namely, the inertial coordinate systems) with respect to which mechanical inertia is isotropic. This does not represent a metaphysical claim about "true" time, or "true" isotropy. It merely relates one class of physical phenomena (electromagnetism) with another (mechanics).

Up to this point we have simply discussed how a system of inertial coordinates is operationally defined on the basis of Newton's Laws (applied quasi-statically). The principle of relativity asserts that, for any material object in any state of motion, there exists a system of inertial coordinates with respect to which the given object is at rest.

The Third Law also serves to establish one fundamental aspect of the relationships between relatively moving inertial coordinate systems. Specifically, the Third Law enables us to assert that if the spatial origin of one inertial coordinate system is moving at velocity v with respect to a second inertial coordinate system, then the spatial origin of the second system is moving at velocity -v with respect to the first. This property is sometimes called reciprocity. This is an important premise for the various derivations of the Lorentz transformation presented in Section 1.

When Einstein developed the general theory of relativity he completely dispensed with the concept of a "force of gravity", and instead interpreted objects under the influence of gravity as simply proceeding, unforced, along the most natural (geodesic) paths. Thus the concept of force, and particularly gravitational force, which was so central to Newton's synthesis, was simply discarded as having no absolute significance. In a larger sense, though, the concept of force is still very important in physics, partly because we continue to employ the classical formulation of mechanics in the limit of low speeds and weak gravity, and partly because it has not proven possible (despite the best efforts of Einstein and others) to do for the other forces of nature what general relativity did for gravity, i.e., express the resulting motions as natural paths through a modified geometry of space and time. Of course, in addition to its strict scientific definitions, the word Force also has many non-technical meanings and connotations - often related to notions of causation - and those non-technical meanings sometimes color people's thinking on the subject. It may be well to recall Maxwell's commentary on Herbert Spenser's talk before the Belfast Section of the British Society in 1874:

Return to Table of Contents