The aberration of light was discovered in 1727 by the astronomer James Bradley, based on an observed seasonal displacement in the apparent positions of stars, especially for stars in the direction perpendicular to the orbital plane of the Earth. This shift in the incident angle of starlight relative to the EarthÆs frame of reference is due to the transverse velocity of the Earth relative to the incoming rays of light. If the Earth intercepts a beam of light that is travelling perpendicularly (in the SunÆs frame of reference) relative to the EarthÆs orbital plane, then, Bradley reasoned, by vector addition the angle a of incidence with respect to the EarthÆs frame would satisfy the equation tan(a ) = v/c, where v is the EarthÆs orbital velocity and c is the speed of light. This analysis, based on the Newtonian corpuscular concept of light, accounted quite well for the data (to the precision that was possible to measure at the time), but the phenomenon of stellar aberration proved to be quite troublesome for theories of electromagnetic propagation based on the wave concept, since it evidently requires the luminiferous ether to be stationary and unaffected by the Earth's passage. Unfortunately, a stationary ether makes it difficult to explain the null results of Michelson's interferometry experiments, which attempted to detect the movement of the Earth through the ether. In Einstein's 1905 paper on special relativity he proposed a completely new basis of explanation for stellar aberration, dispensing with the ether altogether and analyzing the phenomenon from a purely kinematical point of view.
If a photon is emitted from object A at the origin of the xyt coordinates and an angle a relative to the x axis, then at time t1 it will have reached the point
![]()
(Notice that the units have been scaled to make c = 1, so the Minkowski metric for a null interval gives x12 + y12 = t12.) Now consider an object B moving in the positive x direction with velocity v, and being struck by the photon at time t1 as shown below.
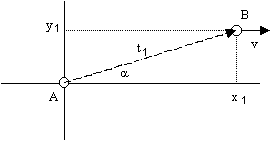
Naturally an observer riding along with B will not see the light ray arriving at an angle a from the x axis, because according to the system of coordinates co-moving with B the source object A has moved in the x direction (but not in the y direction) between the times of transmission and reception of the photon. Since the angle is just the arctangent of the ratio of Dy to Dx of the photon's path, and since value of Dx is different with respect to B's co-moving inertial coordinates whereas Dy is the same, it's clear that the angle of the photon's path is different with respect to B's co-moving coordinates than with respect to A's co-moving coordinates. In general the transformation of the angles of the paths of moving objects from one system of inertial coordinates to another is called aberration.
To determine the angle of the incoming ray with respect to the co-moving inertial coordinates of B, let x'y't' be an orthogonal coordinate system aligned with the xyt coordinates but moving in the positive x direction with velocity v, so that B is at rest in the primed coordinate system. Without loss of generality we can co-locate the origins of the primed and unprimed coordinates systems, so in both systems the photon is emitted at (0,0,0). The endpoint of the photon's path in the primed coordinates can be computed from the unprimed coordinates using the standard Lorentz transformation for a boost in the positive x direction:
![]()
![]()
![]()
Just as we have cos(a) = x1/t1, we also have cos(a') = x1'/t1', and so
![]()
which is the general relativistic aberration formula relating the angles of light rays with respect to relatively moving coordinate systems. Likewise we have sin(a') = y1'/t1', from which we get
![]()
Using these expressions for the sine and cosine of a' it follows that
![]()
Recalling the trigonometric identity tan(z) = sin(2z)/[1+cos(2z)] this gives
![]()
which immediately shows that aberration can be represented by stereographic projection from a sphere to the tangent plane. (This is discussed more fully in Section 2.6.)
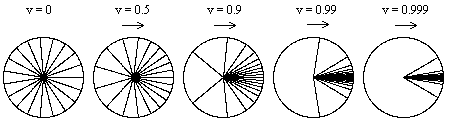
To see the effect of equation (3), suppose that, with respect to the inertial rest frame of a given particle, the rays of starlight incident on the particle are uniformly distributed in all directions. Then suppose the particle is given some speed v in the positive x direction relative to this original isotropic frame, and we evaluate the angles of incidence of those same rays of starlight with respect to the particle's new rest frame. The results, for speeds ranging from 0 to 0.999, are shown in the figure below. (Note that the angles in equation (3) are evaluated between the positive x or x' axis and the positive direction of the light ray.)
The preceding derivation applies to the case when the light is emitted from the unprimed coordinate system at a certain angle and evaluated with respect to the primed coordinate system, which is moving relative to the unprimed system. If instead the light was emitted from B and received at A, we can repeat the above derivation, except that the direction of the light ray is reversed, going now from B to A. The spatial coordinates are all the same but the emission event now occurs at -t1, because it is in the past of event (0,0,0). The result is simply to replace each occurrence of v in the above expressions with -v. Of course, we could reach the same result simply by transposing the primed and unprimed angles in the above expressions.
Incidentally, the aberration formula used by astronomers to evaluate the shift in the apparent positions of stars resulting from the Earth's orbital motion is often expressed in terms of angles with respect to the y axis (instead of the x axis), as shown below
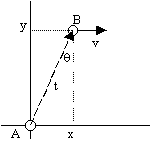
This configuration corresponds to a distant star at A sending starlight to the Earth at B, which is moving nearly perpendicular to the incoming ray. This gives the greatest aberration effect, which explains why the stars furthest from the ecliptic plane experience the greatest aberration. The formula can be found simply by making the substitution a = p - q in equation (1), and noting the trigonometric identity tan(acos(p/2 - x)) = x /![]() . This gives the equivalent form
. This gives the equivalent form
![]()
Another interesting aspect of aberration is illustrated by considering two separate light sources S1 and S2, and two momentarily coincident observers A and B as shown below
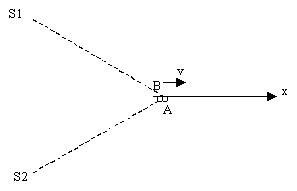
If observer A is stationary with respect to the sources of light, he will see the incoming rays of light striking him from the negative x direction. Thus, the light will impart a small amount of momentum to observer A in the positive x direction. On the other hand, suppose observer B is moving to the right (away from the sources of light) at nearly the speed of light. According to our aberration formula, if B is travelling with a sufficiently great speed, he will see the light from S1 and S2 approaching from the positive x direction, which means that the photons are imparting momentum to B in the negative x direction - even though the light sources are "behind" B. This may seem paradoxical, but the explanation becomes clear when we realize that the x component of the velocities of the incoming light rays is less than c (because (vx)2 = c2 - (vy)2), which means that it's possible for observer B to be moving to the right faster than the incoming photons are moving to the right.
Of course, this effect relies only on the relative motion of the observer and the source, so it works just as well if we regard B as motionless and the light sources S1,S2 moving to the left at near the speed of light. Thus, it might seem that we could use light rays to "pull" an object from behind, and in a sense this is true. However, since the light rays are moving to the right more slowly than the object, they clearly cannot catch up with the object from behind, so they must have been emitted when the object was still to the left of the sources. This illustrates how careful one must be to correctly account for the effective aberration of non-uniformly moving objects, because the simple aberration formulas are based on the assumption that the light source has been in uniform motion for an indefinite period of time. To correctly describe the aberration of non-uniformly moving light sources it is necessary to return to the basic metrical relations.
For example, consider a binary star system in which one large central star is roughly stationary (relative to our Sun), and a smaller companion star is orbiting around the central star with a large angular velocity in a plane normal to the direction to our Sun, as illustrated below.
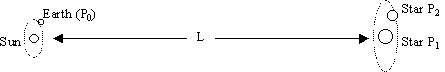
It might seem that the periodic variations in the velocity of the smaller star relative to our Sun would result in significantly different amounts of aberration as viewed from the Earth, causing the two components of the binary star system to appear in separate locations in the sky - which of course is not what is observed. Fortunately, it's easy to show that the correct application of the principles of special relativity, accounting for the non-uniform variations in the orbiting star's velocity, leads to prediction that agree perfectly with observation of binary star systems.
At any moment of observation on Earth we can consider ourselves to be at rest at the point P0 in the momentarily co-moving inertial frame, with respect to which our coordinates are
![]()
Suppose the large central star of a binary pair is at point P1 at a distance L from the Earth with the coordinates
![]()
The fundamental assertion of special relativity is that light travels along null paths, so if a pulse of light is emitted from the star at time t = T and arrives at Earth at time t = 0, we have
![]()
and so
![]()
from which it follows that x1/z1 at time T is ![]() . Thus, for the central star we have the aberration angle
. Thus, for the central star we have the aberration angle
![]()
Now, what about the aberration of the other star in the binary pair, the one that is assumed to be much smaller and revolving at a radius R and angular speed w around the larger star in a plane perpendicular to the Earth? The coordinates of that revolving star at point P2 are
![]()
where q = wt is the angular position of the smaller star in its orbit. The fundamental principle of special relativity is that light travels along null paths, so a pulse of light arriving on Earth at time t = 0 was emitted at time t = T satisfying the relation
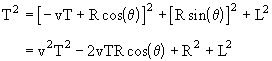
Solving this quadratic for T (and noting that the phase q depends entirely on the arbitrary initial conditions of the orbit) gives
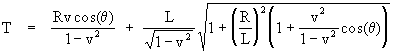
If the radius R of the binary star's orbit is extremely small in comparison with the distance L from those stars to the Earth, and assuming v is not very close to the speed of light, then the quantity inside the square root is essentially equal to 1. Therefore, the tangents of the angles of incidence in the x and y directions are
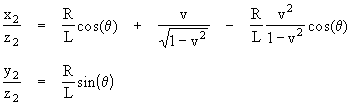
The leading terms in these tangents are obviously just the inherent "static" angular separation between the two stars viewed from the Earth, and the first term in the x tangent is completely negligible (assuming R/L and v are both small compared with 1), so the aberration angle is essentially
![]()
which of course is the same as the aberration of the central star. Indeed, binary stars have been carefully studied for over a century, and the aberrations of the components are consistent with the relativistic predictions for reasonable Keplerian orbits. (Incidentally, recall that Bradley's original formula for aberration was tan(a) = v, whereas the corresponding relativistic equation is sin(a) = v. The actual aberration angles for stars seen from Earth are small enough that the sine and tangent are virtually indistinguishable.)
The experimental results of Michelson and Morley, based on beams of light pointed in various directions with respect to the Earth's motion around the Sun, can also be treated as aberration effects. Let the arm of Michelson's interferometer be of length L, and let it make an angle a with the direction of motion in the rest frame of the arm. We can establish inertial coordinates t,x,y in this frame, in terms of which the light pulse is emitted at t1 = 0, x1 = 0, y1 = 0, reflected at t2 = L, x2 = Lcos(a), y2 = Lsin(a), and arrives back at the origin at t3 = 2L, x3 = 0, y3 = 0. The Lorentz transformation to a system x',y',t' moving with velocity v in the x direction is x' = (x-vt)/g, y' = y, t' = (t-vx)/g where g2 = (1-v2), so the coordinates of the three events are x1' = 0, y1' = 0, t1' = 0, and x2' = L(cos(a)-v)/g, y2' = Lsin(a), t2' = L[1-vcos(a)]/g, and x3' = -2vL/g, y3' = 0, t3' = 2L/g. Hence the total elapsed time in the primed coordinates is 2L/g. Also, the total spatial distance traveled is the sum of the outward distance
![]()
and the return distance
![]()
so the total distance is 2L/g, giving a light speed of 1 regardless of the values of v and a. Of course, the angle of the interferometer arm cannot be a with respect to the primed coordinates. The tangent of the angle equals the arm's y extent divided by its x extent, which gives tan(a) = Lsin(a)/[L(cos(a)] in the arm's rest coordinates. In the primed coordinates the y' extent of the arm is the same as the y extent, Lsin(a), but the x' extent is Lcos(a)g, so the tangent of the arm's angle is tan(a') = tan(a)/g. However, this should not be confused with the angle (in the primed coordinates) of the light pulse as it travels along the arm, because the arm is in motion with respect to the primed coordinates. The outward direction of motion of the light pulse is given by evaluating the primed coordinates of the emission and absorption events at x1,y1 and x2,y2 respectively. Likewise the inward direction of the light pulse is based on the interval from x2,y2 to x3,y3. These give the tangents of the outward and inward angles
![]()
Naturally these are consistent with the result of taking the ratio of equations (1) and (2).