One of the first and most famous examples of the remarkable heuristic power of Einstein's relativistic interpretation was the suggestion that energy and inertial mass are, in a fundamental sense, equivalent. The word "suggestion" is used advisedly, because mass-energy equivalence is not a logically necessary consequence of special relativity. In fact, when combined with the gravitational equivalence principle, it turns out that mass-energy equivalence is technically incompatible with special relativity, and this was one of Einstein's main motivations for developing the general theory. Thus, although Einstein was originally led to the idea of mass-energy equivalence by the special theory, this equivalence ultimately made it necessary to generalize the theory in order to accommodate gravitation consistently.
It should also be mentioned that some kind of equivalence between mass and energy had long been suspected by physicists, even prior to 1905. For example, Poincare had noted that if Galilean relativity was applied to electrodynamics, the equivalence of mass and energy follows. Also, Lorentz had attempted to describe the mass of an electron as a manifestation of electromagnetic energy. (It's interesting that while some people were trying to "explain" electromagnetism as a disturbance in a material medium, others were trying to explain material substances as manifestations of electromagnetism!) However, the fact that mass-energy equivalence emerges so naturally from Einstein's kinematics, applicable to all kinds of mass and energy (not just electrons and electro-magnetism), was mainly responsible for the recognition of this equivalence as a general and fundamental aspect of nature. We'll first give a brief verbal explanation of how this equivalence emerges from Einstein's kinematics, and then follow with a quantitative description.
The basic principle of Einstein's special relativity is that inertial measures of spatial and temporal intervals are such that the velocity of light with respect to those measures is invariant. It follows that relative velocities are not transitively additive from one reference frame to another, and, as a result, the acceleration of an object with respect to one inertial frame must differ from its acceleration with respect to another inertial frame. However, by symmetry, an impact force exerted by two objects (in one spatial dimension) upon each another is equal and opposite, regardless of their relative velocity. These simple considerations lead directly to the idea that inertia (as quantified by mass) is an attribute of energy.
Given an object O of mass m, initially at rest, we apply a force F to the object, giving it an acceleration of F/m. After a while the object has achieved some velocity v, and we continue to apply the constant force F. But now imagine another inertial observer, this one momentarily co-moving with the object at this instant with a velocity v. This other observer sees a stationary object O of mass m subject to a force F, so, on the assumption that the laws of physics are the same in all inertial frames, we know that he will see the object respond with an acceleration of F/m (just as we did). However, due to non-additivity of velocities, the acceleration with respect to our measures of time and space must now be different. Thus, even though we're still applying a force F to the object, its acceleration (relative to our frame) is no longer equal to F/m. In fact, it must be less, and this acceleration must go to zero as v approaches the speed of light. Thus the effective inertia of the object in the direction of its motion increases. During this experiment we can also integrate the force we exerted over the distance traveled by the object, and determine the amount of work (energy) that we imparted to the object in bringing it to the velocity v. With a little algebra we can show that the ratio of the amount of energy we put into the object to the amount by which the object's inertia (units of mass) increased is exactly c2.
To show this quantitatively, suppose the origin of a system of inertial coordinates K0 is moving with speed u0 relative to another system of inertial coordinates K, and if a particle P is moving with speed u (in the same direction as u0) with respect to the K0 coordinates, then the speed of the particle relative to the K coordinates is given by the velocity composition law
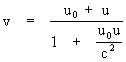
Differentiating with respect to u gives
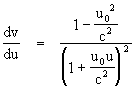
Hence, at the instant when P is momentarily co-moving with the K0 coordinates, we have
![]()
If we let t and t denote the time coordinates of K0 and K respectively, then from the metric (dt)2 = c2(dt)2 - (dx)2 and the fact that v2 = (dx/dt)2 it follows that the incremental lapse of proper time dt along the worldline of P as it advances from t to t + dt is ![]() , so we can divide the above expression by this quantity to give
, so we can divide the above expression by this quantity to give
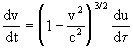
The quantity a = dv/dt is the acceleration of P with respect to the K coordinates, whereas a0 = du / dt is the "rest acceleration" of P with respect to the K0 coordinates (relative to which it is momentarily at rest). Now, by symmetry, a force F exerted between a particle at rest in K on the particle P at rest in K0 must be of equal and opposite magnitude with respect to both frames of reference. Also, by definition, a force of magnitude F applied to a particle of "rest mass" m0 will result in an acceleration of a0 = F/m0 with respect to the reference frame in which the particle is momentarily at rest. Therefore, using the preceding relation between the accelerations with respect to the K0 and K coordinates, we have
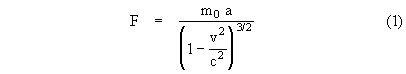
The coefficient of "a" in this expression has sometimes been called the "longitudinal mass", because it represents the effective proportionality between force and acceleration along the direction of action. Now let us define two quantities, p(v) and e(v), which we will call the momentum and kinetic energy of a particle of mass m0 at any relative speed v. These quantities are defined respectively by the integrals of Fdt and Fds over an interval in which the particle is accelerated by a force F from rest to velocity v. The results of these integrations are independent of the pattern of acceleration, so we can assume constant acceleration "a" throughout the interval. Hence the integral of Fdt is evaluated from t = 0 to t = v/a, and since s = (1/2)at2, the integral of Fds is evaluated from s = 0 to s = v2/(2a). In addition, we will define the inertial mass m of the particle as the ratio p/v. Therefore, the inertial mass and the kinetic energy of the particle at any speed v are given by

If the force F were equal to m0a (as in Newtonian mechanics) these two quantities would equal m0 and (1/2)m0v2 respectively. However, we�ve seen that consistency with relativistic kinematics requires the force to be given by equation (1). As a result, the inertial mass is given by m = m0/![]() , so it exceeds the rest mass whenever the particle has non-zero velocity. This increase in inertial mass is exactly proportional to the kinetic energy of the particle, as shown by
, so it exceeds the rest mass whenever the particle has non-zero velocity. This increase in inertial mass is exactly proportional to the kinetic energy of the particle, as shown by
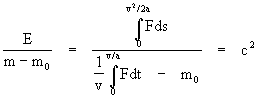
The exact proportionality between the extra inertia and the extra energy of a moving particle naturally suggests that it is the energy itself which has contributed the inertia, and this in turn suggests that all of the particle�s inertia (including its rest inertia m0) corresponds to some form of energy. This leads us to hypothesize a very general and important relation, E = mc2, which signifies a fundamental equivalence between energy and inertial mass. From this we might imagine that all inertia is potentially convertible to energy, although it's worth noting that this does not follow rigorously from the principles of special relativity. It is just a hypothesis suggested by special relativity (as it is also suggested by Maxwell's equations). In 1905 the only experimental test that Einstein could imagine was to see if a lump of "radium salt" loses weight as it gives off radiation, but of course that would never be a complete test, because the radium doesn't decay down to nothing. The same is true with an atomic bomb, i.e., it's really only the binding energy of the atoms (or nucleus, for a hydrogen bomb) that is being converted, so it doesn't demonstrate an entire electron or proton (for example) being converted into energy. However, today we can observe electrons and positrons annihilating each other completely, and yielding amounts of energy precisely in accord with the predictions of special relativity.
Incidentally, the above derivation followed Newton in adopting the Third Law (at least for impulse interactions along the line of motion) as a fundamental postulate, on the basis of symmetry. From this the conservation of momentum can be deduced. However, most modern treatments of relativity proceed in the opposite direction, postulating the conservation of momentum and then deducing something like the Third Law. (There are complications when applying the Third Law to extended interactions, and to interactions in which the forces are not parallel to the direction of motion, due to the ambiguity of simultaneity relations, but the preceding derivation was based solely on interactions that can be modeled as mutual contact events at single points, with the forces parallel to the direction of motion, in which case the Third Law is unproblematic.)
The typical modern approach to relativistic mechanics is to begin by defining momentum as the product of rest mass and velocity. One formal motivation for this definition is that the resulting 3-vector is well-behaved under Lorentz transformations, in the sense that if this quantity is conserved with respect to one inertial frame, it is automatically conserved with respect to all inertial frames (which would not be true if we defined momentum in terms of, say, longitudinal mass). On a more fundamental level, this definition is motivated by the fact that it agrees with non-relativistic momentum in the limit of low velocities. The heuristic technique of deducing the appropriate observable parameters of a theory from the requirement that they match classical observables in the classical limit was used extensively in early development of relativity, but apparently no one dignified the technique with a name until Bohr (characteristically) elevated it to the status of a "principle" in quantum mechanics, where it is known as the "Correspondence Principle".
Based on this definition, the modern approach then simply postulates that momentum is conserved. Then we define relativistic force as the rate of change of momentum. This is Newton's Second Law, and it's motivated largely by the fact that this "force", together with conservation of momentum, implies Newton's Third Law (at least in the case of contact forces).
However, from a purely relativistic standpoint, the definition of momentum as a 3-vector seems incomplete. It's three components are proportional to the derivatives of the three spatial coordinates x,y,z of the object with respect to the proper time t of the object, but what about the coordinate time t? If we let xj, j = 0, 1, 2, 3 denote the coordinates t,x,y,z, then it seems natural to consider the 4-vector
![]()
where m is the rest mass. Then define the relativistic force 4-vector as the proper rate of change of momentum, i.e.,
![]()
Our correspondence principle easily enables us to identify the three components p1, p2, p3 as just our original momentum 3-vector, but now we have an additional component, p0, equal to m(dt/dt). Let's call this component the "energy" E of the object. In full four-dimensional spacetime coordinate time t is related to the object's proper time t according to
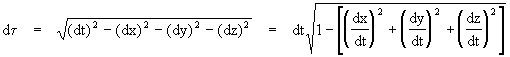
In geometric units (c = 1) the quantity in the square brackets is just v2. Substituting back into our energy definition, we have
![]()
The first term is simply m (or mc2 in normal units), so we interpret this as the rest energy of the mass. This is sometimes presented as a derivation of mass-energy equivalence, but at best it's really just a suggestive heuristic device. The key step in this "derivation" was when we blithely decided to call p0 the "energy" of the object. Strictly speaking, we violated our "correspondence principle" by making this definition, because by correspondence with the low-velocity limit, the energy E of a particle should be something like 1 mv2, and clearly p0 does not reduce to this in the low-speed limit. Nevertheless, we defined p0 as the "energy" E, and since that component equals m when v = 0, we essentially just defined our result E = m (or E = mc2 in ordinary units) for a mass at rest. From this reasoning it isn't clear that this is anything more than a bookkeeping convention, one that could just as well be applied in classical mechanics using some arbitrary squared velocity to convert from units of mass to units of energy. The assertion of physical equivalence between inertial mass and energy has significance only if it is actually possible for the entire mass of an object, including its rest mass, to manifestly exhibit the qualities of energy. Lacking this, the only equivalence between inertial mass and energy that special relativity strictly entails is the "extra" inertia that bodies exhibit when they acquire kinetic energy.
As mentioned above, even the fact that nuclear reactors give off huge amounts of energy does not really substantiate the complete equivalence of energy and inertial mass, because the energy given off in such reactions represents just the binding energy holding the nucleons (protons and nuetrons) together. The binding energy is the amount of energy required to pull a nuclei apart. (The terminology is slightly inapt, because a configuration with high binding energy is actually a low energy configuration, and vice versa.) Of course, protons are all positively charged, so they repell each other by the Coulomb force, but at very small distances the strong nuclear force binds them together. Since each nucleon is attracted to every other nucleon, we might expect the total binding energy of a nucleus comprised of N nucleons to be proportional to N(N-1)/2, which would imply that the binding energy per nucleon would increase linearly with N. However, saturation effects cause the binding energy per nucleon to reach a maximum at for nuclei with N � 60 (e.g., iron), then to decrease slightly as N increases further. As a result, if an atom with (say) N = 230 is split into two atoms, each with N=115, the total binding energy per nucleon is increased, which means the resulting configuration is in a lower energy state than the original configuration. In such circumstances, the two small atoms have slightly less total rest mass than the original large atom, but at the instant of the split the overall "mass-like" quality is conserved, because those two smaller atoms have enormous velocities, precisely such that the total relativistic mass is conserved. (This physical conservation is the main reason the old concept of relativistic mass has never been completely discarded.) If we then slow down those two smaller atoms by absorbing their energy, we end up with two atoms at rest, at which point a little bit of apparent rest mass has disappeared from the universe. On the other hand, it is also possible to fuse two light nuclei (e.g., N = 2) together to give a larger atom with more binding energy, in which case the rest mass of the resulting atom is less than the combined rest masses of the two original atoms. In either case (fission or fusion), a net reduction in rest mass occurs, accompanied by the appearance of an equivalent amount of kinetic energy and radiation. (The actual detailed mechanism by which binding energy, originally a "rest property" with isotropic inertia, becomes a kinetic property representing what we may call relativistic mass with anisotropic inertia, is not well understood.)
Another derivation of mass-energy equivalence is based on consideration of a bound "swarm" of particles, buzzing around with some average velocity. If the swarm is heated (i.e., energy E is added) the particles move faster and thereby gain both longitudinal and transverse mass, so the inertia of the individual particles is anisotropic, but since they are all buzzing around in random directions, the net effect on the stationary swarm (bound together by some unspecified means) is that its resistance to acceleration is isotropic, and its "rest mass" has effectively been increased by E/c2. Of course, such a composite object still consists of elementary particles with some irreducible rest mass, so even this picture doesn't imply complete mass-energy equivalence.
To get complete equivalence we need to imagine something like photons bound together in a swarm. Now, it may appear that equation (2) fails to account for the energy of light, because it gives E proportional to the rest mass m, which is zero for a photon. However, the denominator of (2) is also zero for a photon (because v = 1), so the energy is indeterminate from that expression. However, we know from the study of electro-magnetic radiation that although a photon has no rest mass, it does (according to Maxwell's equations) have momentum, equal to |p| = E (or E/c in conventional units). This suggests that we try to isolate the momentum component from the rest mass component of the energy. To do this, we square equation (2) and expand the simple geometric series as follows
![]()
Excluding the first term, which is purely rest mass, all the remaining terms are divisible by (mv)2, so we can write this is
![]()
The right-most term is simply the squared magnitude of the momentum, so we have the apparently fundamental relation
![]()
consistent with our premise that the E (or E/c in conventional units) equals the magnitude of the momentum |p| for a photon. Of course, electromagnetic waves are classically regarded as linear, meaning that photons don't ordinarily interfere with each other (directly). As Dirac said, "each photon interferes only with itself... interference between two different photons never occurs". However, the non-linear field equations of general relativity enable photons to interact gravitationally with each other. John Wheeler has used the word "geon" to denote a swarm of massless particles bound together by the gravitational field associated with their energy, although he noted that such a configuration would be inherently unstable, viz., it would very rapidly either dissipate or shrink into complete gravitational collapse. Also, it's not clear that any physically realistic situation would lead to such a configuration in the first place, since it would require concentrating an amount of electromagnetic energy equivalent to the mass m within a radius of about r = Gm/c2. For example, to make a geon from the energy equivalent of one electron, it would be necessary to concentrate that energy within a radius of about (6.7)10-58 meters.
An interesting alternative approach to deducing (3) is based directly on the Minkowski metric
![]()
This is applicable both to massive timelike particles and to light. In the case of light we know that the proper time dt and the rest mass m are both zero, but we may postulate that the ratio m/dt remains meaningful even when m and dt individually vanish. Multiplying both sides of the Minkowski line element by the square of this ratio gives immediately
![]()
The first term on the right side is E2 and the remaining three terms are px2, py2, and pz2, so this equation can be written as
![]()
Hence this expression is nothing but the Minkowski spacetime metric multiplied through by (m/dt)2.
Returning to the question of how mass and energy can be regarded as different expressions of the same thing, recall that the energy of a particle with rest mass m0 and speed V is m0/(1-V2)1/2. We can also determine the energy of a particle whose motion is defined as the composition of two orthogonal speeds. Let t,x,y,z denote the inertial coordinates of system S, and let T,X,Y,Z denote the (aligned) inertial coordinates of system S'. In S the particle is moving with speed vy in the positive y direction so its coordinates are
![]()
The Lorentz transformation for a coordinate system S' whose spatial origin is moving with the speed v in the positive x (and X) direction with respect to system S is
![]()
so the coordinates of the particle with respect to the S' system are
![]()
The first of these equations implies t = T(1 - vx2)1/2, so we can substitute for t in the expressions for X and Y to give
![]()
The total squared speed V2 with respect to these coordinates is given by
![]()
Subtracting 1 from both sides and factoring the right hand side, this relativistic composition rule for orthogonal speeds vx and vy can be written in the form
![]()
It follows that the total energy (neglecting stress and other forms of potential energy) of a ring of matter with a rest mass m0 spinning with an intrinsic circumferential speed u and translating with a speed v in the axial direction is
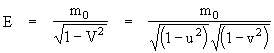
A similar argument applies to translatory motions of the ring in any direction, not just the axial direction. For example, consider motions in the plane of the ring, and focus on the contributions of two diametrically opposed particles (each of rest mass m0/2) on the ring, as illustrated below.
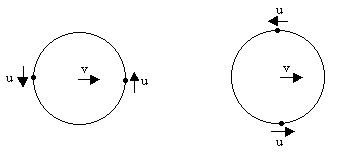
If the circumferential motion of the two particles happens to be perpendicular to the translatory motion of the ring, as shown in the left-hand figure, then the preceding formula for E is applicable, and represents the total energy of the two particles. If, on the other hand, the circumferential motion of the two particles is parallel to the motion of the ring's center, as shown in the right-hand figure, then the two particles have the speeds (v+u)/(1+vu) and (v-u)/(1-vu) respectively, so the combined total energy (i.e., the relativistic mass) of the two particles is given by the sum
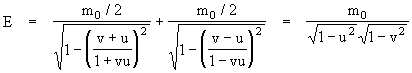
Thus each pair of diametrically opposed particles with equal and opposite intrinsic motions parallel to the extrinsic translatory motion contribute the same total amount of energy as if their intrinsic motions were both perpendicular to the extrinsic motion. Every bound system of particles can be decomposed into pairs of particles with equal and opposite intrinsic motions, and these motions are either parallel or perpendicular or some combination relative to the extrinsic motion of the system, so the preceding analysis shows that the relativistic mass of the bound system of particles is isotropic, and the system behaves just like an object whose rest mass equals the sum of the intrinsic relativistic masses of the constituent particles. (Note again that we are not considering internal stresses and other kinds of potential energy.)
This nicely illustrates how, if the spinning ring was mounted inside a box, we would simply regard the angular kinetic energy of the ring as part of the rest mass M0 of the box with speed v, i.e.,
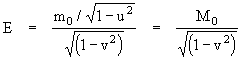
where the "rest mass" of the box is now explicitly dependent on its energy content. This naturally leads to the idea that each original particle might also be regarded as a "box" whose contents are in an excited energy state via some kinetic mode (possibly rotational), and so the "rest mass" m0 of the particle is actually just the relativistic mass of a lesser amount of "true" rest mass, leading to an infinite regress, and the idea that perhaps all matter is really some form of energy.
But does it really make sense to imagine that all the mass (i.e., inertial resistance) is really just energy, and that there is no irreducible rest mass at all? If there is no original kernel of irreducible matter, then what ultimately possesses the energy? Clearly Maxwell's equations can't provide an explanation for any bound state of pure electro-magnetic energy, because they are purely linear, whereas some non-linear interaction is required in order to yield a bound state. This is one of the main reasons that we know Maxwell's equations, by themselves, are not sufficient to account for the structure of the elementary particles of matter. Today we can observe the collision of an electron and a positron, two massive particles of matter, resulting in their mutual annihilation and the release of (apparently) pure energy in the form of photons, seeming to support the view that there is no irreducible "rest mass", and all matter is actually just a manifestation of energy.
To picture how an aggregate of massless energy can have non-zero rest mass, first consider two identical massive particles connected by a massless spring, as illustrated below.
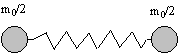
Suppose these particles are oscillating in a simple harmonic motion about their common center of mass, alternately expanding and compressing the spring. The total energy of the system is conserved, but part of the energy oscillates between kinetic energy of the moving particles and potential (stress) energy of the spring. At the point in the cycle when the spring has no tension, the speed of the particles (relative to their common center of mass) is a maximum. At this point the particles have equal and opposite speeds +u and -u, and we've seen that the combined rest mass of this configuration (corresponding to the amount of energy required to accelerate it to a given speed v) is m0/(1-u2)1/2. At other points in the cycle, the particles are at rest with respect to their common center of mass, but the total amount of energy in the system with respect to any given inertial frame is constant, so the effective rest mass of the configuration is constant over the entire cycle. Since the combined rest mass of the two particles themselves (at this point in the cycle) is just m0, the additional rest mass to bring the total configuration up to m0/(1-u2)1/2 must be contributed by the stress energy stored in the "massless" spring. This is one example of a massless entity acquiring rest mass by virtue of its stored energy.
Recall that the energy-momentum vector of a particle is defined as [E, px, py, pz] where E is the total energy and px, py, pz are the components of the momentum, all with respect to some fixed system of inertial coordinates t,x,y,z. The rest mass m0 of the particle is then defined as the Minkowskian "norm" of the energy-momentum vector, i.e.,
![]()
If the particle has rest mass m0, then the components of its energy-momentum vector are
![]()
If the object is moving with speed u, then dt/dt = g = 1/(1-u2)1/2, so the energy component is equal to the transverse relativistic mass. The rest mass of a configuration of arbitrarily moving particles is simply the norm of the sum of their individual energy-momentum vectors. The energy-momentum vectors of two particles with individual rest masses m0 moving with speeds dx/dt = u and dx/dt = -u are [gm0, gm0u, 0, 0] and [gm0, -gm0u, 0, 0], so the sum is [2gm0, 0, 0, 0], which has the norm 2gm0. This is consistent with the previous result, i.e., the rest mass of two particles in equal and opposite motion about the center of the configuration is simply the sum of their (transverse) relativistic masses, i.e., the sum of their energies.
A photon has no rest mass, which implies that the Minkowskian norm of its energy-momentum vector is zero. However, it does not follow that the components of its energy-momentum vector are all zero, because the Minkowskian norm is not positive-definite. For a photon we have E2 - px2 - py2 - pz2 = 0 (where E = hn), so the energy-momentum vectors of two photons, one moving in the positive x direction and the other moving in the negative x direction, are of the form [E, E, 0, 0] and [E, -E, 0, 0] respectively. The Minkowski norms of each of these vectors individually are zero, but the sum of these two vectors is [2E, 0, 0, 0], which has a Minkowski norm of 2E. This shows that the rest mass of two identical photons moving in opposite directions is m0 = 2E = 2hn, even though the individual photons have no rest mass.
If we could imagine a means of binding the two photons together, like the two particles attached to the massless spring, then we could conceive of a bound system with positive rest mass whose constituents have no rest mass. As mentioned previously, in normal circumstances photons do not interact with each other (i.e., they can be superimposed without affecting each other), but we can, in principle, imagine photons bound together by the gravitational field of their energy (geons). The ability of electrons and anti-electrons (positrons) to completely annihilate each other in a release of energy suggests that these actual massive particles are also, in some sense, bound states of pure energy, but the mechanisms or processes that hold an electron together, and that determine its characteristic mass, charge, etc., are not known.
It's worth noting that the definition of "rest mass" is somewhat context-dependent when applied to complex accelerating configurations of entities, because the momentum of such entities depends on the space and time scales on which they are evaluated. For example, we may ask whether the rest mass of a spinning disk should include the kinetic energy associated with its spin. For another example, if the Earth is considered over just a small portion of its orbit around the Sun, we can say that it has linear momentum (with respect to the Sun's inertial rest frame), so the energy of its circumferential motion is excluded from the definition of its rest mass. However, if the Earth is considered as a bound particle during many complete orbits around the Sun, it has no net momentum with respect to the Sun's frame, and in this context the Earth's orbital kinetic energy is included in its "rest mass".
Similarly a "stationary" chunk of lead not microscopically stationary, but in the aggregate, averaged over the characteristic time scale of the mean free oscillation time of a particle, it is stationary, and is treated as such. The temperature of the lead actually represents changes in the states of motion of the constituent particles, but over a suitable length of time the particles are still stationary. We can continue to smaller scales, down to sub-atomic particles comprising individual atoms, and we find that the position and momentum of a particle cannot even be precisely stipulated simultaneously. In each case we must choose a context in order to apply the definition of rest mass.
Physical entities possess multiple modes of excitation (kinetic energy), and some of these modes we may choose (or be forced) to absorb into the definition of the object's "rest mass", because they do not vanish with respect to any inertial reference frame, whereas other modes we may choose (and be able) to exclude from the "rest mass". In order to assess the momentum of complex physical entities in various states of excitation, we must first decide how finely to decompose the entities, and the time intervals over which to make the assessment. The "rest mass" of an entity invariably includes some of what would be called energy or "relativistic mass" if we were working on a lower level of detail.