The problem with the attempted a priori derivation described in the preceding chapter is that it's based on the uncritical assumption of complete 3-way symmetry between the three arguments u,v,w of the composition function. This is a fundamentally misguided approach, because the whole reason for a composition function is that the arguments are not symmetrical. Speeds with respect to any particular frame of reference really are simply additive, by definition, so no special function is required to operate on commensurate speeds. For example, letting A(B) and A(C) denote the speeds of B and C with respect to the reference frame of A, the difference between the speed of B and the speed of C (relative to A) is simply the arithmetic difference A(B) - A(C). However, this is not the speed of C relative to B, which we would denote by B(C). It's essential not to lose sight of the distinction between the addition of speeds and the composition of speeds. Of course, the assumption of Galilean kinematics is that B(C) = A(B) - A(C), which is actually highly non-trivial proposition, because it represents a mixing of inherently incommensurate elements. Quantities of the form A(*) are defined on a different basis than quantities of the form B(*), so the Galilean assumption is like saying if we have ten apples and three are removed, we're left with seven oranges.
There are really six conceptually distinct speeds between three co-linear objects
![]()
By reciprocity we can assert skew symmetry between pairs, such as A(B) = -B(A), thereby reducing the number of independent magnitudes to three, but there are still six conceptually distinct quantities involving three different bases. The function of a composition law is to describe how two quantities on one basis relate to a third quantity on another basis. Thus our composition rule necessarily operates on three arguments such as A(B), A(C), and B(C), i.e., two arguments on one basis and one argument on another basis, so the arguments are not conceptually symmetrical. (Of course, there are really three possible bases, but we can express any three speed on just two bases by invoking reciprocity.)
Now, in order to derive the composition law, we must first examine the basis of our knowledge of the actual speeds of specific objects. Such knowledge can only be based on measurements and observations, but any such knowledge also requires a theoretical framework within which to interpret our observations, and even to tell us what constitutes an observation of speed. A reasonably theory-free concept of speed might be based on the premise that each observer has a concept of his own proper time, i.e., the ordering of immediately sensible events, combined with the idea of reflection. Suppose observer A emits two discrete pulses of a suitable character (i.e., such as have been found to give consistent results) at his proper times T0 and T1, and he associates those with a pair of discrete signals that he subsequently receives (from the direction of some object B) at times T2 and T3. The interval from T2 to T3 will, in general, differ from the interval from T0 to T1. Assuming symmetry between himself and the distant object, observer A concludes that there is a factor relating the time intervals mapped between himself and B. Thus, if we let t0 and t1 denote the inferred arrival times of the signals at B, and if we put DT = T1-T0 , DTr = T3-T2 , and Dt = t1-t0, then by symmetry we have
![]()
so Dt is the geometric mean of DT and DTr . Now we can define the relative speed of B with respect to A as the ratio v = (q-1)/(q+1) where q = (Dt / DT)2. Obviously this is nothing but the "radar speed detection" formula (assuming the signals are electromagnetic waves), but the precise details of the definition are not important. What matters for our purposes is that, regardless of the nature of the signal, any definition of relative velocity must ultimately be based on some such reflective interaction. The concept of relative velocity can be regarded as a correspondence between the observer's experienced linear ordering of events (his proper time) and the respective lapse of proper time inferred for some other object based on the reflected signals.
There is, however, a potential ambiguity in any such definition, arising from the uncertainty in the directionality of time. We've assumed that (Dt)2 and (DT)2 have the same sign, which may seem unobjectionable considering that they're both squared quantities, but unless we wish to rule out non-positive definite metrics a priori, we shouldn't pre-judge the sign of the squared proper time of the distant object. Just as we must be careful to conceptually distinguish between the quantities A(B) and -B(A), we must be equally careful to distinguish between the proper time lapse along A's experience between reception of the two reflected signals and the corresponding lapse of proper time along the experience of the distance object. In both cases we need to clearly separate operations on quantities defined with respect to a common basis, and inferences about quantities defined on different bases. The result of all this (perhaps overly punctilious) hairsplitting is that the primary measured parameter involved in the determination of a distant object's speed is only determined up to sign, meaning we have q = � (Dt)2/(DT)2. Therefore, the derived quantity v, which represents not an absolute parameter, but one defined in terms of coordinate components v = dx/dt, is ambiguous up to inversion, because negating q in v = (q-1)/(q+1) gives 1/v = dt/dx. This is just another way of expressing this symmetry of motion epistemologically, because motion necessarily involves the ratio of a temporal and a spatial interval, but it isn't obvious whether the laws of motion should be expressed in terms of dx/dt or dt/dx. (Ironically, the idea of excluding infinite speeds, which some have suggested as a way toward a rational deduction of the Minkowski metric, actually runs counter to this important symmetry.)
To emphasize the 2+1 symmetry of the three arguments in our speed composition function, let us define the speeds v = A(B), u = A(C), and w = B(C). We seek a function giving w = f(u,v). We still require the function to be single-valued, linear, and uniquely invertible on either of the two arguments, because by reciprocity we can (for example) substitute v' = B(A) in place of v, in which case the two arguments on a common basis are v' and w, so we should get u = f(v',w). The most general such function is the bi-linear form
![]()
for some constants A,B,...,F. We have invoked the 2-way symmetry on the commensurate speeds u,v to equate their coefficients. As in the previous derivation, reciprocity implies w = v when u=0, and this forces C=E=0 and B=F. Also, if w=0 we require u=-v, which forces A=0. Clearly B is non-zero (or the function would vanish identically), so we can divide numerator and denominator by B to give
![]()
where k = C/B. Not surprisingly, we've reached essentially the same composition rule as we did at the end of Section 1.7, but now it's properly expressed in terms of an arithmetical function of commensurate quantities. Likewise when we solve this relation for u, we are making the conceptual transformation of v from A(B) to -B(A), so that the composition function always operates on commensurate quantities. (There is an interesting parallel between these scruples and the need for covariant differentiation on curved manifolds, due to the fact that partial differentiation doesn't yield a tensor, because we're evaluating a difference in a vector field on two different bases, as discussed in Part 4 of the Appendix.)
Of course, we still haven't succeeded in determining the value of k. As before, if k = 0 we have the Galilean composition rule, and if k = 1 we have the Einsteinian composition rule. However, we haven't yet specified whether the arguments u,v are "speeds" in the sense of dx/dt or in the sense of dt/dx. Any consistent choice of sign conventions for the reflected speed parameter q when defining the commensurate arguments u,v should lead to the same result. This implies that if we substitute 1/u and 1/v in place of u and v, the function f should remain unchanged. Thus the complete set of symmetries we impose on our linear speed composition law can be summarized as
![]()
It may not be immediately obvious that the right hand condition can consistently be met, and indeed it can't if we select the Galilean parameter k = 0, because then we have
![]()
Hence the Galilean composition rule does not support our symmetry requirements. However, somewhat remarkably, with k = 1 we find that the Einsteinian composition function gives
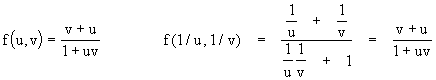
so in fact this rule is consistent with all three of the symmetry requirements. On this basis we arrive at the unique composition law with k=1, which (with appropriate choices of signs for the speeds) can be expressed in the form
![]()
To more clearly exhibit this peculiar 2+1 symmetry of this velocity composition law, note that it can be expressed in multiplicative form as
![]()
where vij denotes the speed of object j with respect to object i. Clearly if we replace any two of the speeds with their reciprocals, the relation remains unchanged. On the other hand, if we replace just one, or all three, of the speeds with their reciprocals, their product is still unity, but the sign is negated. Thus, one way of expressing the full symmetry of this relation would be to square both sides, giving the result
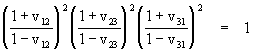
which is completely invariant under any replacement of one or more speeds with their respective reciprocals. Naturally we can extend the product of factors of the form (1+vij)/(1- vij) to any cyclical sequence of relative speeds between any number of colinear points.
To see another interesting aspect of this symmetry, notice that we've been working with speed parameters u,v,w defined as ratios of space over time, i.e., derivatives of the form dx/dt, but we could just as well have been using parameters of the reciprocal form dt/dx. Nothing in our development of (1) would be affected, so we would arrive at an equation of exactly the same form, i.e., we would get
![]()
where U=1/u, V=1/v, and W=1/w. Although this is formally the same as (1), there is a difference, at least assuming we distinguish between time and space. Thus, by applying the same reasoning we arrive at physically different rules of speed composition. The only difference in the premises was an arbitrary choice of whether to use dx/dt or dt/dx. This places us in an odd circumstance, since our arbitrary choice evidently affects the content but not the form of our kinematical laws.
If we let u,v (or U,V) denote the commensurate primary speed parameters and w (or W) the inferred secondary parameter, then (1) implies that all inferred secondary parameters will be of the form w because, whether we choose to regard u,v or U,V as the primary parameters, our inferred secondary parameters will be given by
![]()
both of which yield w for the inferred speed. On the other hand, (2) implies that all inferred secondary parameters will be of the form W = 1/w, because the governing equation will be
![]()
If the first law applies, then any consistent observer will deduce space-over-time measures for all secondary motions, whereas if the second law applies he will deduce time-over space measures for all secondary motions. These two sets of laws have an interesting dual relationship, and can be summarize as follows
q(u,v,w) = uvw + u + v + w = 0
Q(u,v,w) = uv + uw + vw + 1 = 0
Notice that splits up the linear terms into odd and even degrees. Consequently we have
(1+u)(1+v)(1+w) = Q(u,v,w) + q(u,v,w)
(1- u)(1- v)(1- w) = Q(u,v,w) - q(u,v,w)
Whichever law we select, either Q or q will be identically zero, leading again to the multiplicative form
![]()
where the plus sign corresponds to the Q law, and the minus sign to the q law. This represents an interesting kind of "symmetry breaking", because if we take the square of this expression we subsume both laws (and treat time and space interchangeably), whereas taking the square root introduces an ambiguous sign, with the result being a distinction between space and time (although still a subtle one).
Given that we have settled on the composition law u' = (u+v)/(1+uv) for co-linear speeds, what can we say about the transformation of the coordinates x and t themselves under the action of the velocity v? The composition law can be written in the form vuu'+u'- u = v, which has a natural factorization if we multiply through by v and subtract 1 from both sides, giving
![]()
If u and u' are taken to be the spatio-temporal ratios x/t and x'/t', the above relation can be written in the form
![]()
On the other hand, remembering that we can insert the reciprocals of any two of the quantities u, u', v without disturbing the equality, we can take u and u' to be the temporal-spatial ratios t/x and t'/x' in (3) to give
![]()
These last two equations immediately give
![]()
Treating the primed and unprimed frames equivalently, and recalling that v' = - v, we see that (4) has a perfectly symmetrical factorization, so we exploit this factorization to give the transformation equations
![]()
![]()
These are the Lorentz transformations for velocity v in the x direction. The y and z coordinates are unaffected, so we have y' = y and z' = z. From this it follows that the quantity t2 - x2 - y2 - z2 is invariant under a general Lorentz transformation, so we have arrived at the full Minkowski spacetime metric.
To determine the full velocity composition law for two systems of aligned coordinates k and K, the latter moving in the positive x direction with velocity v relative to the former, we can without loss of generality make the origins of the two systems both coincide with a point P0 on the subject worldline, and let P1 denote a subsequent point on that worldline with k system coordinates dt,dx,dy,dz. By definition the velocity components of that worldline with respect to k are ux = dx/dt, uy = dy/dt, and uz = dz/dt. The coordinates of P1 with respect to the K system are given by the Lorentz transformation for a simple boost v in the x direction:
![]()
where g = ![]() . Therefore, the velocity components of the worldline with respect to the K system are
. Therefore, the velocity components of the worldline with respect to the K system are
![]()
![]()
![]()
It's interesting to review from a slightly different perspective some of the abstract considerations leading to the basic velocity transformation law. Recall that for any two systems of inertial coordinates A and B we let A(B) denote the velocity of the origin of B with respect to the A coordinates. The relativity of position can be expressed by the identity
A(A) = 0
for any system A, and the relativity of velocity can be expressed by the skew symmetry
A(B) + B(A) = 0
for any two systems A and B. (This was referred to earlier as the reciprocity condition A(B) = -B(A).) The next step is to consider the cyclic sum involving three systems, A, B, and C. This is the key relation, because all higher-order relations can be reduced to this. If acceleration were relative, we would expect the cyclic symmetry A(B) + B(C) + C(A) = 0, which is a linear function of all three components. However, since acceleration is absolute, it's to be expected that the actual relation is non-linear in each of the three components. So, instead of vanishing, we need the right side of this sum to be a symmetric function of the terms. The only other odd elementary symmetric function of three quantities is the product of all three, so we're led to the relation
A(B) + B(C) + C(A) = -A(B) B(C) C(A)
which can be regarded as the law of inertia. Since there is only one odd elementary symmetric function of one variable, and likewise for two variables, the case of three variables is the first for which there exists a non-tautological expression of this form.
We also note a formal correspondence with De Morgan's law for logical statements. Letting sums denote logical ORs (unions), products denote logical ANDs (intersections), and overbars denote logical negation, we have
![]()
for any three logical variables X,Y,Z. Also, using the skew symmetry property we can "negate" each velocity on the right hand side of the previous expression to give
A(B) + B(C) + C(A) = B(A) C(B) A(C)
From this standpoint the right hand side is analagous to the "logical negation" of the left hand side, which makes the relation analagous to setting the quantity equal to zero. The justification for regarding this relation as the source of inertia becomes more clear in Section 2.3, which describes how the relativistic composition law for velocities accounts for the increasing inertia of an accelerating object. This leads to the supposition that all inertia is ultimately a consequence the non-linearity of velocity compositions.