In retrospect it's easy to see that the Galilean view of reference frame compositions was not free of conceptual difficulties, because the group of Galilean compositions doesn't provide a logical structure for quantifying a definite and complete separation between every possible pair of events. It allows us to consider the spatial separation between strictly simultaneous events, but the spatial separation between non-simultaneous events separated by a time increment Dt is totally undefined. There exist perfectly valid reference frames in which two non-simultaneous events are at precisely the same spatial location, and other frames in which they are arbitrarily far apart. Still, in all of those frames (according to Galilean relativity), the time interval remains Dt. Thus, there is no definite combined spatial and temporal separation, in spite of the fact that we clearly intuit a definite physical difference between our distance from "the office tomorrow" and our distance from "the Andromeda galaxy tomorrow". Admittedly we could postulate a universal preferred reference frame for the purpose of assessing the true and complete separations between events, but such a postulate is entirely foreign to the logical structure of Galilean space and time, to say nothing of the fact that it's operationally meaningless without some prescription for actually determining the preferred frame, which classical mechanics never provided.
In 1908 Minkowski delivered a famous lecture in which he argued that the phenomena discovered by Lorentz and clarified by Einstein might have been inferred from first principles, if only we had given more careful thought to the foundations of classical geometry and mechanics. He pointed out two physical invariances which we ordinarily take for granted. The first is the invariance of quantities of the form
under arbitrary rotations, where x,y,z are rectangular space coordinates. This applies to rotations of the coordinate system, and also to re-orientations of physical objects, and the group of all transformations (not counting reflections) that leave this quantity invariant is called the Euclidean group. It includes not only rotations, but arbitrary spatial offsets as well, i.e., we can select any point as the origin. This invariance is derived from experience by each person as we observe and come to expect that the lengths of physical objects are independent of orientation (all else being equal). As Minkowski said at the beginning of his lecture, "the views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength".
The second invariance that humans historically derived from experience was that the laws of mechanics governing the motions of material objects are unchanged if we everywhere make the substitutions
where a,b,g are arbitrary constants (corresponding to the speeds in the x, y, and z directions respectively). Historically this dynamic invariance was viewed as entirely separate from the geometric invariance, but suppose we combine them by making the above substitutions in the geometric invariant to give the quantity
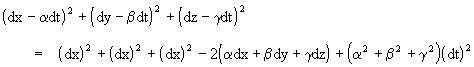
Obviously this is not invariant under arbitrary rotations with arbitrary constants a,b,g, but it suggests that the true geometrical invariant might be of this form for some restricted non-zero values of those constants. In order for this quantity to be invariant under purely spatial rotations (i.e., with dt = 0), the term adx + bdy + gdz must vanish, which means the vector (a,b,g) must be orthogonal to (dx,dy,dz).
Now, if we choose a,b,g such that the squared magnitude of the vector (a,b,g) is positive, then the resulting overall quantity would simply be a four-dimensional Euclidean invariant. Since we know that time is not simply another space dimension, we are led to suppose that the squared magnitude is some negative constant, which we denote as -c2. Then our proposed invariant quantity is
For any fixed value of the constant c, we will denote by Gc the group of transformations that leave this quantity unchanged. If we let c go to infinity, the temporal increment dt must be invariant, leaving just the original Euclidean group for the spatial increments. Thus the space and time components are de-coupled, in accord with Galilean relativity. Minkowski called this limiting case G , and remarked that
Since Gc is mathematically much more intelligible than G, it looks as though the thought might have struck some mathematician, fancy-free, that after all, as a matter of fact, natural phenomena do not possess invariance with the group G , but rather with the group Gc, with c being finite and determinate, but in ordinary units of measure extremely great. Such a premonition would have been an extraordinary triumph for pure mathematics. Well, mathematics, though it now can display only staircase wit, has the satisfaction of being wise after the event... to grasp the far-reaching consequences of such a metamorphosis of our concept of nature.
Minkowski is here clearly suggesting that Lorentz invariance might have been deduced from apriori considerations, appealing to mathematical "intelligibility" as a criterion for the laws of nature. Einstein himself eschewed the temptation to retroactively deduce Lorentz invariance from first principles, choosing instead to base his original presentation of special relativity on two empirically-founded principles, the first being none other than the classical principle of relativity, and the second being the proposition that the speed of light is the same with respect to any system of inertial coordinates, independent of the motion of the source. This second principle often strikes people as arbitrary and unwarranted (rather like Euclid's "fifth postulate", as discussed in Section 3.1), and there have been numerous attempts to deduce it from some more fundamental principle. For example, it's been argued that the light speed postulate is actually redundant to the relativity principle itself, since if we regard Maxwell's equations as fundamental laws of physics, and we regard the permeability m0 and permittivity e0 of the vacuum as invariant constants of those laws in any uniformly moving frame of reference, then it follows that the speed of light in a vacuum is c = 
with respect to every uniformly moving system of coordinates. The problem with this line of reasoning is that Maxwell's equations are not valid when expressed in terms of an arbitrary uniformly moving system of coordinates. In particular, they are not invariant under a Galilean transformation - despite the fact that systems of coordinates related by such a transformation are uniformly moving with respect to each other. (Maxwell himself recognized that the equations of electromagnetism, unlike Newton's equations of mechanics, were not invariant under Galilean "boosts"; in fact he proposed various experiments to exploit this lack of invariance in order to measure the "absolute velocity" of the Earth relative to the luminiferous ether. See Section 3.3 for one example.)
Furthermore, we cannot assume, apriori, that m0 and e0 are invariant with respect to changes in reference frame. (Actually m0 is an assigned value, but e0 must be measured.) For example, see Maxwell's discussion of the ratio of electrostatic to electromagnetic units in sections 768 and 769 of his Treatise, in which he predicts that two parallel sheets of electric charge, both moving in their own planes in the same direction with velocity c (which he believed was possible in principle), would exert no net force on each other - a prediction that would be plainly absurd if the velocities of the sheets could be defined with respect to any arbitrary frame of reference. The means of empirically determining e0 involve observations of the force between charged plates, and Maxwell clearly believed these measurements must be made with the apparatus "at rest" with respect to the ether in order to yield the true and isotropic value of e0. According to Maxwell's conception, if these measurements were performed with an apparatus travelling at some significant fraction of the speed of light, the results would not only differ from the result at rest, they would also vary depending on the orientation of the plates relative to the direction of the absolute velocity of the apparatus.
Of course, the efforts of Maxwell and others to devise empirical methods for measuring the absolute rest frame (either by measuring anisotropies in the speed of light or by detecting variations in the electromagnetic properties of the vacuum) were doomed to failure, because even though it's true that the equations of electromagnetism are not invariant under Galilean transformations, it is also true that those equations are invariant with respect to every system of inertial coordinates. Maxwell (along with everyone else before Einstein) would have regarded those two propositions as logically contradictory, because he assumed inertial coordinate systems are related by Galilean transformations. Einstein was the first person to recognize that this is not so, i.e., to recognize that relatively moving inertial coordinate systems are actually related by Lorentz transformations.
Maxwell's equations are suggestive of the invariance of c not because of any aspect of the equations themselves, but only because of the added circumstance that we are unable to physically identify any particular frame of reference for the application of those equations. The most readily observed instance of this inability to single out a unique reference frame for Maxwell's equations is the empirical invariance of light speed with respect to every inertial system of coordinates, from which we can infer the invariance of e0. Hence attempts to deduce the invariance of light speed from Maxwell's equations are fundamentally misguided. Furthermore, as discussed in Section 1.6, we know (as did Einstein) that Maxwell's equations are not fundamental, since they don't encompass quantum photo-electric effects (for example), whereas the Minkowski structure of spacetime (representing the invariance of the local characteristic speed of light) evidently is fundamental, even in the context of quantum electrodynamics. This strongly supports Einstein's decision to base his kinematics on the light speed principle itself. (As in the case of Euclid's decision to specify a "fifth postulate" for his theory of geometry, we can only marvel in retrospect at the underlying insight and maturity that this decision reveals.)
Another argument that is sometimes advanced in support of the second postulate is based on the notion of causality. If the future is to be determined by (and only by) the past, then (the argument goes) no object or information can move infinitely fast, and from this restriction people have tried to infer the existence of a finite upper bound on speeds, which would then lead to the Lorentz transformations. One problem with this line of reasoning is that it's based on a principle (causality) that is not unambiguously self-evident. Indeed, if certain objects could move infinitely fast, we might expect to find the universe populated with large sets of indistinguishable particles, all of which are really instances of a small number of prototypes moving infinitely fast from place to place, so that they each occupy numerous locations at all times. This may sound implausible until we recall that the universe actually is populated by apparently indistinguishable electrons and protons, and in fact according to quantum mechanics the individual identities of those particles are ambiguous in many circumstances. Richard Feynman once seriously toyed with the idea that there is only a single electron in the universe, weaving its way back and forth through time. Admittedly there are problems with such theories, but the point is that causality and the directionality of time are far from being straightforward principles.
Moreover, even if we agree to exclude infinite speeds, i.e., that the composition of any two finite speeds must yield a finite speed, we haven't really accomplished anything, because the Galilean composition law has this same property. Every real number is finite, but it does not follow that there must be some finite upper bound on the real numbers. More fundamentally, it's important to recognize that the Minkowski structure of spacetime doesn't, by itself, automatically rule out speeds above the characteristic speed c (nor does it imply temporal asymmetry). Strictly speaking, a separate assumption is required to rule out "tachyons". Thus, we can't really say that Minkowskian spacetime is prima facie any more consistent with causality than is Galilean spacetime.
A more persuasive argument for a finite upper bound on speeds can be based on the idea of locality, as mentioned in our review of the shortcomings of the Galilean transformation rule. If the spatial ordering of events is to have any absolute significance, in spite of the fact that distance can be transformed away by motion, it seems that there must be some definite limit on speeds. Also, the continuity and identity of objects from one instant to the next (ignoring the lessons of quantum mechanics) is most intelligible in the context of a unified spacetime manifold with a definite non-singular connection, which implies a finite upper bound on speeds. This is in the spirit of Minkowski's 1908 lecture in which he urged the greater "mathematical intelligibility" of the Lorentzian group as opposed to the Galilean group of transformations.
For a typical derivation of the Lorentz transformation in this formalistic spirit, we may begin with the basic Galilean program of seeking to identify coordinate systems with respect to which physical phenomena are optimally simple. We have the fundamental principle that for any material object in any state of motion there exists a system of space and time coordinates with respect to which the object is instantaneously at rest and Newton's laws of inertial motion hold good (at least quasi-statically). Such a system is called an inertial rest frame coordinate system of the object. Let x,t denote inertial rest frame coordinates of one object, and let x',t' denote inertial rest frame coordinates of another object moving with a speed v in the positive x direction relative to the x,t coordinates. How are these two coordinate systems related? We can arrange for the origins of the coordinate systems to coincide. Also, since these coordinate systems are defined such that an object in uniform motion with respect to one such system must be in uniform motion with respect to all such systems, and such that inertia isotropic, it follows that they must be linearly related by the general form x' = Ax + Bt and t' = Cx + Dt, where A,B,C,D are constants for a given value of v. The differential form of these equations is dx' = Adx + Bdt and dt' = Cdx + Ddt.
Now, since the second object is stationary at the origin of the x',t' coordinates, it's position is always x' = 0, so the first transformation equation gives 0 = Adx + Bdt, which implies dx/dt = -B/A = v and hence B = -Av. Also, if we solve the two transformation equations for x and t we get (AD-BC)x = Dx' - Bt', (AD-BC)t = -Cx' + A. Since the first object is moving with velocity -v relative to the x',t' coordinates we have -v = dx'/dt' = B/D, which implies B = -Dv and hence A = D. Furthermore, reciprocity demands that the determinant AD - BC = A2 + vAC of the transformation must equal unity, so we have C = (1-A2)/(vA). Combining all these facts, a linear, reciprocal, unitary transformation from one system of inertial coordinates to another must be of the form
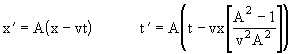
It only remains to determine the value of A (as a function of v), which we can do by fixing the quantity in the square brackets. Letting f(v) denote this quantity for any given v, the transformation can be written in the form
The simplest possibility is that f(v) is a constant, in which case we can normalize its magnitude by a suitable choice of space and time units so that the only three fundamentally distinct possibilities to consider are -1, 0, and +1. Setting f(v) to 0 gives the familiar Galilean transformation x' = x - vt, t' = t. This is highly asymmetrical between the time and space parameters, in the sense that it makes the transformed space parameter a function of both the space coordinate and the time coordinate of the original system, whereas the transformed time coordinate is dependent only on the time coordinate of the original system.
Alternatively, if we set f(v) = -1, we have the transformation
Letting q denote the angle that the line from the origin to the point (x,t) makes with the t axis, then tan(q) = v = dx/dt, and we have the trigonometric identities cos(q) = 1/(1+v2)1/2 and sin(q) = v/(1+v2)1/2. Therefore, this transformation can be written in the form
which is just a Euclidean rotation in the xt plane. Under this transformation the quantity (dx)2 + (dt)2 = (dx')2 + (dt')2 is invariant. This transformation is clearly too symmetrical between x and t, because know from experience that we cannot turn around in time as easily as we can turn around in space.
The only remaining alternative (assuming a constant f(v)) is to set f(v) = 1, which gives the transformation
Although perfectly symmetrical, this maintains the absolute distinction between spatial and temporal intervals. This can be parameterized as a hyperbolic rotation
and we have the invariant quantity (dx)2 - (dt)2 = (dx')2 - (dt')2 for any given interval. It's hardly surprising that this transformation, rather than either the Galilean transformation or the Euclidean transformation, gives the actual relationship between space and time coordinate systems with respect to which inertia is directionally symmetrical and inertial motion is linear. From purely formal considerations we can see that the Galilean transformation, given by setting f(v) = 0, is incomplete and has no spacetime invariant, whereas the Euclidean transformation, given by setting f(v) = -1, makes no distinction at all between space and time. Only the Lorentzian transformation, given by setting f(v) = 1, has completely satisfactory properties from an abstract point of view, which is presumably why Minkowski referred to it as "more intelligible".
As plausible as such arguments may be, they don't amount to a logical deduction, and one is left with the impression that we have not succeeded in identifying any fundamental principle or symmetry that uniquely selects Lorentzian spacetime rather than Galilean space and time. Accordingly, most writers on the subject have concluded (reluctantly) that Einstein's light speed postulate, or something like it, is indispensable for deriving special relativity, and that we can be persuaded to adopt such a postulate only by empirical facts. Indeed, later in the same paper where Minkowski exercised his staircase wit, he admitted that "the impulse and true motivation for assuming the group Gc came from the fact that the differential equation for the propagation of light [i.e., the wave equation] in empty space possesses the group Gc", and he referred back to Voigt's 1887 paper (see Section 1.4).
Nevertheless, it's still interesting to explore the various rational "intelligibility" arguments that can be put forward as to why space and time must be Minkowskian. A typical approach is to begin with three speeds u,v,w representing the pairwise speeds between three co-linear particles, and to seek a composition law of the form Q(u,v,w) = 0 relating these speeds. It's easy to make the case that it should be possible to uniquely solve this function explicitly for any of the speeds in terms of the other two, which implies that Q must be linear in all three of its arguments. The most general linear function of three variables is
Q(u,v,w) = Auvw + Buv + Cuw + Dvw + Eu + Fv + Gw + H
where A,B,...H are constants. Treating the speeds symmetrically requires B = C = D and E = F = G. Also, if any two of the speeds is 0 we require the third speed to be 0 (transitivity), so we have H = 0. Also, if any one of the speeds, say u, is 0, then we require v = -w (reciprocity), but with u = 0 and v = -w the formula reduces to -Dv2 + Fv - Gv = 0, and since F = G (= E) this is just Dv2 = 0, so it follows that B = C = D = 0. Hence the most general function that satisfies our requirements of linearity, 3-way symmetry, transitivity, and reciprocity is Q(u,v,w) = Auvw + E(u+v+w) = 0. It's clear that E must be non-zero (since otherwise general reciprocity would not be imposed when any one of the variables vanished), so we can divide this function by E, and let k denote A/E, to give
It only remains to determine the value of k. Obviously if k = 0 we have the Galilean composition law, whereas if k = 1 we have the Einsteinian composition law. How are we to decide? In the next section we consider the problem from a slightly different perspective, and focus on a unique symmetry that arises only with k = 1.